. Piotr 10: Mam pytanie jest to zadanie z matury zadania.info Proszę o ocenienie tylko Oblicz jaka może być najmniejsza możliwa długość przeciwprostokątnej trójkąta prostokątnego o polu S. Czy c=2√S

Godzio: Tak.

Piotr 10: Dobra dzięki . Męczyłem się i wyszło

Godzio: Długie rozwiązanie, czy ciężko było wpaść? Bo rozwiązanie samo w sobie jest pół linijkowe.

Piotr 10: Cięźko było wpaść, a rozwiązanie to nie aż takie długie. W skrócie tylko napiszę ( nie chce pisać calego rozwiazania, bo jutro zadania.info je pokaze ) c²=(a+b)² − 2ab , gdzie 2ab=4S , a potem wyraziłem a i b za pomocą c i funkcji sinα i cosα Tak samo robiłeś czy inaczej ?

Godzio: c² = a² + b² ≤ 2ab = 4S ⇒ c = 2√S Równość zachodzi dla a = b, wtedy wartość jest najmniejsza. I tyle

Piotr 10: Wychodzi na to, ze dla trójkąta prostokatnego rownoramiennego tak zachodzi

Piotr 10: a²+b² ≤ 2ab ?

Godzio: Nierówność w drugą stronę oczywiście.

Piotr 10: Ok. Widzę, szybki sposób Mój kilka linijek dłuższy

Piotr 10: Bym mógł jeszcze spytać się o jedno zadanie ze stereometrii z tej matury czy nie za bardzo( chodzi mi o wynik )?

Godzio: No pytaj

Piotr 10: Podstawą ostrosłupa ABCD jest trójkąt równoramienny ABC, w którym IABI=IACI=7, IBCI=6. Krawędzie boczne maja długości: IDAI=7 , IDBI=IDCI=5. Oblicz objetosc tego ostrosłupa. W skrócie 'odwróciłem sobie ten ostrosłup. I mam podstawe BDC a krawedzie boczne sa rowne

	9√31
i wyszlo mi ze V=
	2

Godzio: Wynik poprawny

Piotr 10: Ok. Dzięki wielkie. Czyli mogę spokojnie na maturze w maju sobie ten ostrosłup ''odwrócić'' , tak jak w tym zadaniu ?

Godzio: Tak, możesz, ważne, żeby się nie pomylić w oznaczeniach.

Piotr 10: Kolejne pytanie jeśli mam w treści dwa pierwiastki roznych znakow to czy x=0 jest rozwiązaniem czy nie ? Moim zdaniem nie jest, bo 0 nie jest ani dodatnia ani ujemna

Godzio: Jest tak jak piszesz.

Piotr 10: Ok.

kyrtap: Piotr jaki masz wynik w zadaniu pierwszym?

Piotr 10: k∊ ( − 3 ; 7 )

Piotr 10: jak chcesz mozemy wymienic sie wynikami

kyrtap: tak ale mi inaczej wyszło tak samo z objętością a nie wiem co źle zrobiłem lipa trochę

Piotr 10: Z bryła fajne zadanie, masz podpowiedź na górze tego postu

kyrtap: tak tylko myślę że dobrze policzyłem tylko nędzny mi wynik wyszedł

Piotr 10:

	1
to tak Pp=12 a R=3		i potem z Pitagorasa liczysz H
	8

H²=7² − R²

kyrtap: z hornera wyliczyłem pole podstawy i wyszło mi 6√10

Damo93: Piotr 10 ja już też skończyłem ale szczerze mówiąc nie zrobiłem zad.1 nie wiem jak się za nie zabrać a i w zad.2 nie do końca.. resztę mam zrobioną

kyrtap: dobra nieważne nie wiem czemu mi tak wyszło potem tak samo wyliczełem R i z tw pitagorasa pojechałem

kyrtap: z kombinatoryką 120 liczb?

Damo93: tak

Piotr 10: tak

kyrtap: P(A∪B) = 0.8?

Piotr 10: To w pierwszym trzeba graficznie zrobic

Piotr 10: tak

Damo93: w zad.5 R=10√2 ?

Piotr 10: Podam swoje odpowiedzi wszystkie na raz

kyrtap: oki

Damo93: sekunda ja w 12 mam 0,9

Piotr 10: 1. k∊ ( − 3 ; 7 ) 2. a = −6; b=8 ; c=6 ; d = −3 3. dowód

	4
4. m∊< − 2; −		) ∪ (0;+∞).
	5

5.R=10√2

	π		4π		5π		11π
6. x∊{		;		;		;		}
	3		3		6		6

7. c=2√S 8.120 9. m= 1,5

	9√31
10. V=
	2

11. k= −6 , n=9

	4
12. P(A∪B)=
	5

Ja mam takie wyniki

kyrtap: czemu mi w 10 źle mi wyszło

Piotr 10: Źle pole podstawy masz zapewne P_p=12

kyrtap: no ale z Hornera powinno tak samo wyjść

	7 + 7 + 6
p =		= 20
	2

P = √ 10(10 −7)(10 − 7) (10 −6) = 6√10

Piotr 10: Zauważ ze to nic Ci nie da. Musisz ten ostroslup obrocic tak, zeby podstawa to byla Δ BDC o bokach 5, 5 , 6 a wtedy krawedzie boczne beda sobie rowne i wynosic 7

kyrtap: jejku zapomniałem o fakcie że mogę wyliczyć długość promienia opisanego na trójkącie wtedy i tylko wtedy gdy wszystkie krawędzie boczne są tej samej długości

kyrtap: dzięki za oświecenie mnie kurde lipa będzie na maturze

Piotr 10: A jak reszta wyników ? Możesz porownac z moimi ?

kyrtap: oprócz 1 mam tak samo

Piotr 10: Ja to w pierwszym zrobiłem tak Ix+5I = −k²+4k + 26 −k²+4k + 26 = p Ix+5I=p Narysowalem wykres funkcji f(x)=Ix+5I potem dla p > 5 beda dwa rozwiazania roznych znakow −k²+4k + 26 > 5 i to rozwiazalem

kyrtap: ale chyba ja źle te pierwsze zinterpretowałem bo ja to zapisałem tak : Ix +5I = −k² +4k +26 i wtedy to co po prawej stronie wziąłem że jest większe od zera

kyrtap: to pewnie masz dobrze jeszcze raz to przeanalizuje

Piotr 10: takie zadanka najlepiej graficznie robic

kyrtap: z tym 7 trochę się męczyłem

kyrtap: zapamiętam

Piotr 10: Ja tez sie meczylem z tym 7 Ale Godzio mnie osmieszyl tak prostym rozwiazaniem . ja to robilem inaczej ( dluzej )

Piotr 10: Z rownaiem trygonometrycznym to podzieliles przez cosx ?

kyrtap: tak

kyrtap: innej metody na to nie widzę

Piotr 10: . ciekawa matura,

Piotr 10: ja tez podzililem przez cosx . tak szybko sie robi

kyrtap: nom powiem szczerze że fajna byłem zadowolony z ostatniego bo lubię te zbiorki zawsze robić

kyrtap: ale z tym ostrosłupem się wkurzyłem że zapomniałem o tej własności i to niecały miesiąc przed maturą

Piotr 10: Spoko, po to są te matury zeby sobie poprzypominac ; ). Może akurat cos takiego sie trafi

kyrtap: nom w sumie masz rację nawet może teraz lepiej się takie coś trafiło niż na maturze

Draghan: Przepraszam, że Wam przerwę, ale chciałbym czegoś się dowiedzieć... Nawiązując do wypowiedzi Piotr 10: "Kolejne pytanie jeśli mam w treści dwa pierwiastki roznych znakow to czy x=0 jest rozwiązaniem czy nie ?" Ja mam pytanie "pokrewne" Czy jeśli w treści zadania napisane jest "funkcja kwadratowa ma dwa pierwiastki tych samych znaków", to czy przypadek x₁ = x₂ = 0 łapie się w założeniach?

Piotr 10: Moim zdaniem to nie bo 0 to liczba niedodatnia i nieujemna ( nie ma ona znakow )

Piotr 10: Jeszcze będzie jedna matura z zadania. info za 2 tyg

Draghan: Hm. Ale właśnie. Skoro nie ma znaku, to 0 jest tego samego znaku, co 0 (żadnego)

kyrtap: już tylko jedna tak na ten rok Piotrze?

Piotr 10: Mam w zeszycie zapisane tak Dwa rozne pierwiastki jednakowych znakow a≠0 Δ > 0 x₁*x₂ > 0 a więc 0 nie wlicza sie

Piotr 10: no jeszcze 26 kwietnia i koniec, za tyg nie ma ( bo swieta sa )

Draghan: Oki. Ale to mi nie da i tak spokoju Dobrze, że PW tego pytania nie widział, bo znowu by się niepotrzebnie zdenerwował Dzięki, Piotrze

kyrtap: ja już tylko w poniedziałek do szkoły idę

kyrtap: a jak tam wy ?

Piotr 10: Ja to rzadko chodzę, lepiej w domu siedziec i uczyc sie

kyrtap: no ja teraz poważnie się biorę

kyrtap: w sumie jeszcze trochę czasu jest na powtórki

kyrtap: a mam pytanie nierówności trygonometryczne też są na maturze bo jeszcze nie widziałem aby były na jakiejś maturze?

Piotr 10: no mogą być. tez sie nie spotkalem jeszcze w arkuszach

Marcin: Są w programie dla szkół średnich, ale specjalnie się ich nie spodziewaj

kyrtap: no mam nadzieję ale lepiej kilka przećwiczę przed maturą

Draghan: Ja od zeszłego roku nie byłem w szkole Nierówności trygonometryczne... Jak się odpowiedni wykres zrobi, to chyba nie problem taką nierówność rozwiązać?

jerey: dobra przekmina z tą bryłą Piotrze, też sie głowiłem i zastanawiałem sie jak znaleźć spodek wysokości. Nie wpadł bym na to

zawodus: Dlatego, że nierówności zgodnie ze standardami nie mogą być zbyt skomplikowane To po co dawać na rozszerzeniu?

zawodus: Zadanie podobne było na zeszłorocznej maturze też z zadania.info.

kyrtap: tutaj z tego co widzę forumowicze powinni z rozszerzenia mieć powyżej 90% ja się nie wliczam do nich oczywiście raczej do nich

jerey: ja tez nie

zawodus: Z polskiego zatem będzie zdecydowanie gorzej

zawodus: Ja też nie

kyrtap: haha masz rację z podstawowej miałem 65%

Marcin: Jak wszyscy, to i ja

Draghan: Ja mam nadzieję, że będę miał te 60%. Byłoby dobrze 70% to już super

kyrtap: ostatnie pytanie odnośnie tego zadania z promieniem liczyliście go jako R = abc/4P ?

zawodus: Można w ten sposób

kyrtap: to sponio

kyrtap: ej a na maturze można wnosić jedzenie?

Piotr 10: nie ; / , tylko wodę podobno

kyrtap: szkoda trochę

zawodus: Możesz wnieść wszystko, ale czy pozwolą ci pisać maturę to już różnie Chyba nie. To tylko 3 godziny Wcinasz kebaba przed maturą i jest ok

kyrtap: chyba tak zrobię

Draghan: O pustym żołądku się lepiej myśli Info potwierdzone praktyką w wielogodzinnych turniejach szachowych

zawodus: O pustym żołądku, bo jesteś tak głodny, że sobie mówisz (wygram lub przegram, ale to musi się skończyć )

Draghan: Heh Nie no Po pierwsze ja gram tylko w szachy szybkie A po drugie, w czasie zawodów można nawet sobie wyjść na kebaba (oczywiście możesz przegrać partię, jak twój czas upłynie ) Mogę się podzielić dwoma radami. Gorzej się myśli z pełnym żołądkiem,ponadto jest obawa, że może złapać jakaś biegunka w czasie egzaminu Lepiej zjeść śniadanko dość skromne i nawodnić odpowiednio organizm (to poprawia ogólną wydolność organizmu, nie tylko mózgu), ale też nie można przesadzić − żeby potem co trzy minuty nie biegać do toalety

5-latek: Draghan czesc calkiem powaznie no to jesli (+)0=0 i (−)0=0 to 0 jest roznych znakow ?

5-latek: https://matematykaszkolna.pl/forum/246375.html i moze spojrzyj tu co napisalem

Draghan: Witaj. 5−latek Te znaki zer stosuje się tylko przy badaniu granic funkcji, czy coś takiego, prawda? Skoro jest 0 różnych znaków... To...? To wtedy taka f−cja o x₁ = x₂ = 0 (czyli − de facto f(x) = x²) ma dwa rozwiązania identycznych znaków? Ech, nie chcę znów takiej dyskusji, jak pod tym linkiem Się znowu ktoś będzie niepotrzebnie denerwował... Poza tym, im bardziej ktoś stara się to wytłumaczyć, na tym wyższy poziom wchodzimy... A ja mam tylko średnie wykształcenie, w dodatku z matmą podstawową. Więc też tym więcej rzeczy mogę nie łapać, wykazując tym samym pewną ignorancję, w stosunku do rozmówcy.

5-latek: Powiem CI tak . Ja tez mam srednie (tylko wczesniejsze Wlasnie dlatego te cymbaly z CKE powinny to bardzo dokladnie opisac w swoich wytycznych a nie wprowadzac zametu Kiedy ja siee uczylem to jesli bylo dwa pierwiastki to byla delta >0

Draghan: Ech. Naprawdę bym chciał być porządnie wyedukowany Osobiście jestem przerażony tym ciągłym obniżaniem poprzeczki. Za parę pokoleń (heh − jak dobrze pójdzie, bo jeśli nie, to nawet szybciej) będą same cymbały wszędzie Jeśli będzie takie zadanie na maturze, napiszę komentarz i obliczę 2 razy Chociaż tak też źle, bo mogę żadnych punktów nie dostać

Damo93: Jednokładność z analitycznej też raczej nie ma co się spodziewać na maturze majowej?

5-latek: Opiniodawca ksiazki D.M Zakrzewskich pt Jak rozwiazywac zadania (algebra trygonometria jest Pani mgr Olga Stande jest ona autorka wraz z A Eurenhaut ksiazki do matematyki z ktorej ja sie mialem zaszczyt uczyc Pisza oni tak sa dwie konwencje okreslania liczby pierwiastkow rownania kadratowego dla delta =0 Czasem mowi sie ze rownanie takie posiada jeden pierwiastek podwojny czsem ze dwa rowne pierwiastki . Oni przyjeli ta 1 konwencje To jesli sa dwa rowne pierwiastki to znaczy ze sa tych samych znakow TO oznacza ze jeli wyjdzie pierwiastek x₀=0 to bedzie tak jak piszsesz. To jest moja opinia . Pozdrawiam

Piotr 10: Damo93 było na maturze w 2008 roku https://matematykaszkolna.pl/strona/1771.html

Damo93: akurat to zadanko to tylko podstawienie do wzoru chodzi mi o coś bardziej skomplikowanego

Damo93: zadania raczej mało popularne moim zdaniem/

5-latek: Damo 93 pewnie nie bedzie

Piotr 10: Albo może zadanie z trójkątem, na probnej było

Damo93: jak dla mnie to jakieś proste może być, oby za bardzo nie kombinowali to będzie OK

Draghan: 5−latek, dla Ciebie Czyli pozostało ubezpieczyć się ładnym zestawem założeń To może tak:

⎧	a ≠ 0
⎨	Δ ≥ 0
⎩	x1*x2 > 0

v

⎧	a ≠ 0
⎨	Δ = 0
⎩	x1*x2 = 0

5-latek: Ja bym tak zrobil teraz jak bym pisal mature Ale moze zapytajmy jeszce o opinie Panie Mile lub Ete Pozdrawiam obie Panie One sa bardziej kompetentne w tym temacie niz ja

jerey: soryy, ze tutaj, juz nie chce zakładac nowego wątku a zadanko dotyczny dzisiejszej matury z zadania info(rozszerzona). zrobił ktos rowanie trygonometryczne?

Piotr 10: tak, ja zrobilem

zawodus: Pewnie zrobił

kyrtap: me too

Piotr 10: Musisz po prostu zauważyć, ze cos x ≠ 0 z założenia to wiemy, więc możesz podzielic obustronnie przez cosx

razor: chyba wiekszosc osob tutaj a z czym masz problem?

jerey: czyli rownanie bedzie takiej postaci;? 3tg²x=2√3tgx+3? i teraz zmienna i rozwiązywac?

Piotr 10: tak tgx= t

jerey: dzieki Piotrze

kyrtap: ej mam pytanie mam k = 6 lub k = −6 i się zastanawiam trochę bo ja z tego rozwiązania wziąłem k = 6 sugerując się że suma jest ujemna czy to jest do końca poprawne

Piotr 10: Z zależności wyjdzie, ze q=3 lub q=−3 I teraz wstawiasz to do sumy na ciąg geometryczny szesciu poczatkowych wyrazów i dla q=3

Piotr 10: i dla q=3 będzie sprzeczność

jerey:

π		4π		5π		11π
	,		,		,		. z rownania?
3		3		6		6

jeszcze z wielomianem miałem problemy. Moglbys przedstawic swoje rozwiązanie? byłbym wdzieczny albo chociaz pokrótce wytłumaczył jak to zrobic

Piotr 10: też tak mam zbytnio nie chce pisac rozwiazania ale moge dac podpowiedź wyznacz wpierw reszte z dzielenia wielomianu Q(x) przez R(x). I wiemy, ze P(x)=Q(X)*(−x+f)+A(x), gdzie A(x) to reszta z dzielenia i teraz sie zastanow dlaczego jest (−x+f), a potem...

jerey: mam reszte, ale co to jest to (−x+f) bo nie rozumiem tego zapisu

Piotr 10: Mamy wielomian P(x)=3x⁵ − 5x⁴+ax³+bx²+cx+d a Q(x)= − 3x⁴+2x³+8x² I teraz dzieląc wielomian P(x) przez Q(x) otrzymamy wielomian stopnia pierwszego a więc możemy zapisać P(x)=Q(x)*( o*x+f)+A(x) od razu można zauważyc, ze o= − 1

jerey: aaa juz wiem, nie ogarnąłem . dobra, dalej juz sam dokoncze, dzieki wielkie

Piotr 10: Ja już idę. W razie czego wyżej ja podałem jaki wynik mi wyszedł ( ale nie wiem czy to jest ok ). Pozdrawiam

jerey: ja rowniez dzieki wielkie jeszcze raz, czesc!

Marcin:

	√25110
Ale się pobawiłem z tym ostrosłupem Jego wysokość wyszła mi		, ale później z
	40

tego doszedłem do tego samego wyniku co Piotrek i inni Pewnie dlatego, że ja wcale tego ostrosłupa nie obracałem

jerey: to jakim cudem znalazłeś spodek wysokości i wysokośc

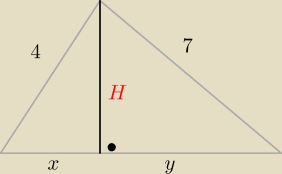
Marcin: x+y to wysokość trójkąta równoramiennego w podstawie. czyli x+y=2√10 Tak to zrobiłem

jerey:

Marcin: nie ważne jak, ważne że wynik się zgadza

jerey:

Draghan: Linijką zmierzył

Marcin: Spodek wysokości nie był mi tu potrzebny Draghan

Bogdan: Wielokrotnie słyszałem wypowiadane z zadowoleniem stwierdzenie: "Nieważne jak, ważne, że wynik się zgadza". Nie godzę się z takim podejściem do rozpatrywanego problemu. Otóż właśnie ważne jest jak. Bardzo ważne. Bez urazy Marcinie.

Draghan: Mi pozostaje się jedynie zgodzić z przedmówcą, bo prawdę rzecze

Marcin: Mogłem to dać w cudzysłowie, bo się z tym nie utożsamiam Też się z Tobą Bogdanie zgadzam. Chociaż to nie oznacza, że mój sposób rozwiązania jest zły

Jacek: Ja mam pytanie do zadania 11 jak Wy je zrobiliście, bo mi ono kompletnie nie chce wyjść?

Jacek: dobra juz ogarnąłem

tomek: Panowie jak zrobiliście 3? ten dowód?

razor: Trójkąty podobne

Piotr 10: Ja to z tw. na temat odcinka laczacego środki w trojkacie

zawodus: Jakie środki?

Marcin: Odcinek łączący środki boków w trójkącie jest równoległy do jednej z podstaw tego trójkąta. O to pewnie chodzi Piotrkowi

Draghan: Jednym odcinkiem da się połączyć boki w trójkącie? Zaginasz tym odcinkiem przestrzeń, czy jak?

zawodus: Marcin masz chęć na zadanko?

Marcin: Chęć mam, ale z czasem średnio Ale możesz coś rzucić to jak dam radę to popatrzę

Marcin: Draghan, a nie da się?

Draghan: Eeee... A trzeci to co, to już nie należy do trójkąta?

zawodus: Marcin jednym odcinkiem w "normalnym" trójkącie nie da się połączyć środków wszystkich boków

Marcin: Ale mi chodzi o środki dwóch boków. Myślałem że sam na to wpadniesz

zawodus: Ja wiem, ale miliony nie

Marcin: Wybaczcie miliony to nieporozumienie. Czuję że was zawiodłem

Draghan: * miliony wybaczają *