aaaa P@weł: Bogdan, jestes? pomozesz?

Bogdan: Jestem , w czym Ci pomóc?

P@weł: ZAdanie: https://matematykaszkolna.pl/forum/245801.html pomagał mi w nim ZKS ale mam problem z dokonczeniem Chodzi mi glownie o zapis z " 8 kwi 2014 16:17 " JA juz okreslilem przedzialy dla m: Δ>0 Δ=0 Δ<0 tylko nie rozumiem wlasnie tego zapisu z " 8 kwi 2014 16:17 " nie wiem jak okreslic liczbe rozwiazan dla poszczegolnyc przedzialow

P@weł: hmm?

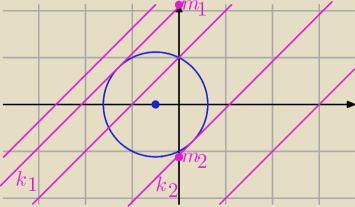
Bogdan: Może ta ilustracja pomoże. dla y = x + m i x² + y² + x − 1 = 0 Po sprowadzeniu do równania kwadratowego otrzymujemy Δ = −4m + 4m + 9 dla Δ = 0 otrzymujemy dwie styczne:

	1 + √10		1 − √10
k1: y = x +		, k2: y = x +		,
	2		2

	1 + √10		1 − √10
czyli dla m−1 =		lub m2 =		jest jedno rozwiązanie
	2		2

dla Δ < 0 nie ma rozwiązań, prosta y = x + m nie ma punktów spólnych z okręgierm, wtedy m > m₁ lub m < m₂ dla Δ > 0 są dwa rozwiązania, prosta y = x + m jest sieczną okręgu, w tym przypadku m∊(m₁, m₂)

Bogdan: czyli dla m₁ = ..., a nie ... dla m − 1 w piątym wierszu od dołu

ZKS:

	1 − √10		1 + √10
Bogdan tylko że dla m = 0 ∊ (		;		) mamy trzy
	2		2

rozwiązania tak samo jak dla m = 1.

Bogdan: Pokazuję tylko fragment dotyczący okręgu i prostej