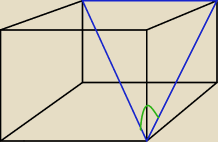
Graniastosłup prawidłowy czworokątny Filipo: Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 4 a przekątna graniastosłupa ma długość 9. Oblicz objętość graniastosłupa oraz cosinus kąta nachylenia przekątnej graniastosłupa do ściany bocznej.

jakubs: Wyznacz przekątną podstawy i z twierdzenia Pitagorasa wysokość i masz objętość.

Filipo: Pierwszą część zadania zrobiłem, V=112. Chodzi mi o cosinus kąta nachylenia przekątnej do ściany bocznej, tak jak na rysunku.

Filipo: Czyli ten zielony kąt.

Filipo: Ktoś pomoże...?

jakubs: Z twierdzenia cosinusów.

zawodus: to ten kąt

Filipo: Może coś więcej niż tylko jedno zdanie?

Filipo: Ja wiem, że to ten kąt.

zawodus: Znasz twierdzenie cosinusów? Jak nie to czas poznać... https://matematykaszkolna.pl/strona/543.html Napisałem 4 zdania.

Filipo: Przecież to jest trójkąt prostokątny i mogę wyliczyć to z funkcji trygonometrycznych, już to zrobiłem. Twierdzenie cosinusów pasuje tutaj jak świnia do gwiazd. Nie dziękuję za pomoc.

jakubs: Ktoś oferuje swoją pomoc, a Ty jeszcze z takimi tekstami. Nie zdziw się, jeśli kiedyś nie otrzymasz pomocy przy zadaniu.

zawodus: Jak jesteś taki "mądry" to po co prosisz o pomoc? Poczekamy, zobaczymy... czy tak wszystko umiesz....

Filipo: Nie oferuje swojej pomocy tylko nie czyta treści zadania ze zrozumieniem i wyjeżdża z pierwszą lepszą mądrością, która tutaj nie pasuje nie doprowadzi do rozwiązania tego zadania. Proszę, rozwiąż to twierdzeniem cosinusów jeśliś taki mądry.

jakubs: Masz dane trzy boki, więc wystarczy podstawić do wzoru. Nie ja mądry nie jestem tak dla Twojej informacji.

Filipo: Nie mam danych trzech boków. I widzisz, to jest właśnie brak czytania ze zrozumieniem.

zawodus: jakubs daj sobie spokój. Najlepiej nie odpisywać wcale.

Filipo: No ale dlaczego odpuszczasz? No zrób to zadanie tak jak chciałeś je zrobić Nie ma danego 3 boku. Skoro już zaczęliście rozwiązywać to skończcie a nie "daj sobie spokój".

zawodus: trzeci bok z Pitagorasa można zdobyć... nie będę tracił czasu na rozwiązywanie. Jest wiele osób, które bardziej potrzebuje pomocy.

Filipo: zawodus: A reszta to z zajęć wyleciała? 10 kwi 21:13 Rzeczywiście, pomagasz jak cholera

zawodus: Mogę pomagać jak chcę...

Damo93: skoro masz krawędź podstawy i przekątną graniastosłupa to możesz policzy wysokość, potem liczysz przekątną ściany bocznej i cosα =

	przekątna−graniastosłupa
	Przekątna−ściany−bocznej

Filipo: Cosinus wyszedł mi √65/9

Mila: Filippo, bez nerwów. a=4− dł. krawędzi podstawy d=9 − dł przekątnej gran. p=4√2 − dł przekątnej podstawy 9²=p²+H² H²=81−16*2 H²=49 H=7 q− przekątna ściany bocznej q²=H²+a² oblicz Teraz możesz liczyc cosinus jak Ci się podoba, jednak wiem, że bardzo wielu uczniów liczy to z twierdzenia cosinusów. ( Po prostu nie szuka tam kąta prostego a ma 3 boki Δ)

Eta: Mila

Filipo: Czyli wychodzi tak jak policzyłem.

Filipo: Dziękuję bardzo Mila, jak zwykle niezawodna

Mila: Długo pisałam, (miałam telefon) i nie widziałam Eto Waszych wpisów. Filippo poprawi się i bedzie grzeczny.