gem
Radek:
Na prostej y = − 3x+ 2 wyznacz punkt, którego suma kwadratów odległości od osi układu
współrzędnych jest najmniejsza
Chciałem zrobić że
Oś ox (x,o)
Oś oy (o,y)
(x−x)2+(0−3x+2)2+(0−x)2+(y−3x+2)2 ale to y wszystko psuje
8 kwi 22:38
Eta:
A(x, −3x+2)
odl . A od osiOX jest : |y| a od osi OY : |x|
f(x)=|x|2+|y|2 = x2+(2−3x)2 =..........
8 kwi 22:45
Radek:
Ale czemu nie liczymy tego ze wzoru na długość odcinka ? Mogła by Pani wyjaśnić ?
8 kwi 22:49
Mila:
Witaj Eto, już to kiedyś tłumaczyłam Radkowi, widać zapomniał.
8 kwi 22:58
int:
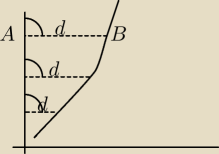
W zadaniu jest odległość od osi, a nie od początku układu, dlatego
d
AB=
√(xB−xA)2+(yB−yA)2, a ponieważ AB jest równoległe do osi OX to y
A=y
B więc
wychodzi d
AB=
√x2=|x|.
Tak samo dla drugiej osi.
8 kwi 22:58
Radek:
Nie mogę znaleźć linku więc jeszcze raz. I tłumaczyła Pani podobne zadanie.
8 kwi 22:59
Radek:
Wyznacz współrzędne punktu P leżącego na wykresie funkcji y = 7x−x2−15 , dla którego suma
odległości od osi układu współrzędnych jest najmniejsza
A tutaj to nie działa |x|+|y|
8 kwi 23:20
Rafał28:
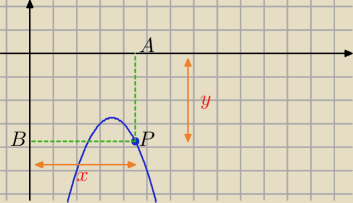
Wybierasz dowolny punkt P(x, 7x−x
2−15). Ta druga współrzędna to y.
Odległości od układu współrzędnych. Najmniejszy odcinek od punktu P do osi OX, OY, czyli:
|AP| oraz |BP|, gdzie punkt A ma taką samą współrzędna x co punkt P oraz
punkt B ma taką samą współrzędną y co punkt P
A(x, 0) oraz B(0, 7x−x
2−15) oraz P(x, 7x−x
2−15)
Teraz wzór na odległość dwóch punktów
|AB| + |BP|
Wyjdzie jakaś tam funkcja kwadratowa.
8 kwi 23:30
Mila:
Zrobiłeś z podpowiedzią Ety? Czy dalej drążymy?
8 kwi 23:32
Radek:
Cześć

A czemu pierwszym sposobem nie można ?
8 kwi 23:32
Radek:
| | 3 | | 1 | |
Tamto zadanie zrobione A=( |
| , |
| ) |
| | 5 | | 5 | |
8 kwi 23:32
Radek: ?
8 kwi 23:41
Mila:
Suma odległości punktu P(x, 7x−x
2−15) od osi układu wsp.
g(x)=|x|+|−x
2+7x−15|
Parabola leży pod osią OX , czyli przyjmuje wartośći ujemne. ( masz wykres
Rafała)
1) |x|=x dla x>0
|−x
2+7x−15|=x
2−7x+15
g(x)=x+x
2−7x+15
g(x)=x
2−6x+15
g(x) ma najmniejszą wartość dla x=3
f(x)=−x
2+7x−15
f(3)=−9+7*3−15=−3
P=(3,−3)
8 kwi 23:56
Radek:
Ale ja mam suma odległości a nie suma kwadratów więc jak opuszczać moduł nie mogę podnieś
przecież do kwadratu ?
9 kwi 00:00
Radek: ?
9 kwi 16:44
Radek: ?
9 kwi 17:22
Radek: ?
9 kwi 19:02
Radek: podpowie ktoś ? co stało się z |x|2 ? czemu nie uwzględniamy ?
9 kwi 19:18
Mila:
Punkt P(x, 7x−x2−15)
A=(x,0)
B=(0,y)=(0,7x−x2−15)
|BP|=√(x−0)2+(7x−x2−15−(7x−x2−15)2=√x2+02=|x|
|AP|=√(x−x)2+(7x−x2−15−0)2=√02+(7x−x2−15)2=√(7x−x2−15)2=|7x−x2−15|
9 kwi 21:08
9 kwi 21:09
Radek:
Ale z tego sposobu który Pani wyżej podała
23:56 to jak dokończyć ?
9 kwi 21:22
Mila:
Tam masz skończone, czytaj uważnie i analizuj, co tam napisałam.
9 kwi 21:25
Radek:
Czyli odległość jest dodatnia więc moduł bez zmiany a w drugim też chyba bez zmiany powinno być
?
9 kwi 21:27
Mila:
Odległość jest dodatnia , ale wartość f(x)<0 , bo parabola leży pod osią OX i dlatego zmieniamy
znak .
9 kwi 22:12
Radek:
Dziękuję, zrozumiałem i zakodowałem

9 kwi 22:13
Mila: Dobrze.
9 kwi 22:37
 W zadaniu jest odległość od osi, a nie od początku układu, dlatego
dAB=√(xB−xA)2+(yB−yA)2, a ponieważ AB jest równoległe do osi OX to yA=yB więc
wychodzi dAB=√x2=|x|.
Tak samo dla drugiej osi.
W zadaniu jest odległość od osi, a nie od początku układu, dlatego
dAB=√(xB−xA)2+(yB−yA)2, a ponieważ AB jest równoległe do osi OX to yA=yB więc
wychodzi dAB=√x2=|x|.
Tak samo dla drugiej osi.
 Wybierasz dowolny punkt P(x, 7x−x2−15). Ta druga współrzędna to y.
Odległości od układu współrzędnych. Najmniejszy odcinek od punktu P do osi OX, OY, czyli:
|AP| oraz |BP|, gdzie punkt A ma taką samą współrzędna x co punkt P oraz
punkt B ma taką samą współrzędną y co punkt P
A(x, 0) oraz B(0, 7x−x2−15) oraz P(x, 7x−x2−15)
Teraz wzór na odległość dwóch punktów
|AB| + |BP|
Wyjdzie jakaś tam funkcja kwadratowa.
Wybierasz dowolny punkt P(x, 7x−x2−15). Ta druga współrzędna to y.
Odległości od układu współrzędnych. Najmniejszy odcinek od punktu P do osi OX, OY, czyli:
|AP| oraz |BP|, gdzie punkt A ma taką samą współrzędna x co punkt P oraz
punkt B ma taką samą współrzędną y co punkt P
A(x, 0) oraz B(0, 7x−x2−15) oraz P(x, 7x−x2−15)
Teraz wzór na odległość dwóch punktów
|AB| + |BP|
Wyjdzie jakaś tam funkcja kwadratowa.
 A czemu pierwszym sposobem nie można ?
A czemu pierwszym sposobem nie można ?
