9 kwi 20:49
bezendu: ?
9 kwi 21:02
Mila:
Mieszaj zadania, najpierw łatwe, potem trudniejsze.
Jaki obowiązujący zbiór masz w szkole, o ile wiem, to dla technikum, są dobre zbiory z
geometrią.
Ja mam z wydawnictwa "Nowik", pięknie wytłumaczona geometria.
9 kwi 21:19
bezendu:
Ja już do szkoły nie chodzę. Miałem matematyka z plusem. Mieszając zadania nie wyrobię się z
całym materiałem..
9 kwi 21:20
Mila:
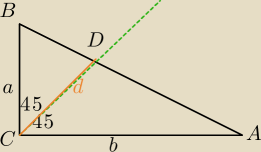
Jeszcze raz inny sposób:
1) Znaleźć długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o
przyprostokątnych
a i b.
| | 1 | | 1 | |
PΔABC= |
| *a*d*sin(45)+ |
| *b*d*sin(45)⇔ |
| | 2 | | 2 | |
| 1 | | 1 | | 1 | |
| *a*d*sin(45)+ |
| *b*d*sin(45)= |
| a*b⇔/*2 |
| 2 | | 2 | | 2 | |
2)
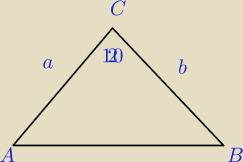
W trójkącie ABC dane są boki a i b oraz kąt C=120o.
Oblicz długość odcinka dwusiecznej kąta C.
9 kwi 21:41
bezendu:
|AB|
2=a
2+b
2+ab
|AB|
2=ab(a+b)
|AB|=
√ab(a+b)
Czy to jest ok do tej pory ?
9 kwi 21:44
Mila:
ab(a+b)≠a2+b2+ab
A gdzie dwusieczna, popatrz na rozwiązanie zadania (1).
I po co obliczasz AB, jaki masz plan?
Uwaga: ( poradnikach, tablicach, masz tak)
Naprzeciw wierzchołka A leży bok oznaczony literą a.
Naprzeciw wierzchołka B leży bok oznaczony literą b.
Naprzeciw wierzchołka C leży bok oznaczony literą c.
9 kwi 21:52
bezendu:
Zęby obliczyć długość boku AB i potem z pola ?
1) sposób był z podobieństwa w innym wątku.
9 kwi 21:54
Eta:
Bolą Cię
zęby?

9 kwi 21:55
bezendu:
Żeby policzyć długość odcinka AB i potem z pola.
9 kwi 21:56
Eta:

9 kwi 21:56
bezendu:

9 kwi 21:57
Mila:
bezendu, sposób dostosowujemy do zadania.
Dzisiaj podałam inny sposób,który pozwoli Ci rozwiązać to zadanie z trójkątem rozwartokątnym
bez zbędnych komplikacji.
Jeżeli coś piszę do Ciebie, to z celem.
Pole inaczej oblicz, bez boku AB.
9 kwi 22:04
bezendu:
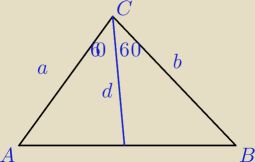
| 1 | | 1 | |
| *a*d*sin60+ |
| *db*sin60 |
| 2 | | 2 | |
| √3 | | √3 | |
| ad+ |
| db=U{√3}[4}ab /*4 |
| 4 | | 4 | |
√3ad+
√3db=
√3ab
ad+db=ab
d(a+b)=ab
9 kwi 22:06
bezendu:
Wiem, że chcesz mi pomóc i to doceniam. I jestem bardzo wdzięczny za to !
9 kwi 22:06
Mila:
Teraz dobrze , w drugiej linijce brak:
P=..
9 kwi 22:17
bezendu:
To już coś więcej wiem. I zapamiętam

9 kwi 22:19
Mila:
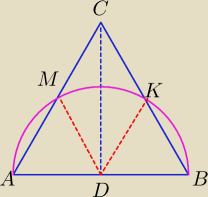
3) Na boku a trójkąta równobocznego , jako na średnicy zakreślono okrąg .
Znaleźć pole części trójkąta zawartej wewnątrz okręgu.
Najpierw zrób konstrukcję na kartce.
9 kwi 22:37
bezendu:
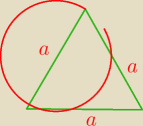
Na kartce wyszło, tutaj nie koniecznie
9 kwi 22:45
Mila:
9 kwi 22:56
bezendu:
ADM i KDB są równoboczne ?
9 kwi 23:00
Mila:
Tak, zastanów się dlaczego.
9 kwi 23:08
bezendu:
Na pewno AD to promień i MD również a kąty po 60 więc jest równoboczny
9 kwi 23:10
Mila:
|AD|=|MD|=r ⇔ΔAMD jest Δ równoramiennym⇔∡A=∡M=600⇒∡D=60o
Licz dalej pole figury.
9 kwi 23:21
9 kwi 23:24
Mila:
Nie.
2*PΔ+Pwycinka
9 kwi 23:37
9 kwi 23:41
Mila:
Dobrze.
Dobranoc.
9 kwi 23:56
bezendu:
Dziękuję jutro poproszę o większą porcję trudniejszych

Dobranoc.
9 kwi 23:58
Mila:
1) Stosunek pola rombu do pola koła wpisanego w ten romb wynosi 8:π.
Oblicz miarę kąta ostrego tego rombu.
2)Stosunek długości przekątnych rombu wynosi 3:4.
Oblicz stosunek pola rombu do koła wpisanego w ten romb.
10 kwi 15:28
Mila: 3) rozwiąż nierówność:
b)
| | x2−2x+1 | | x−1 | |
| |
| |+| |
| |−12<0 |
| | x2−4x+4 | | x−2 | |
10 kwi 15:31
Mila:
4) Dla jakich wartości parametru m∊R równanie :
| 5 | | 3 | |
| = |
| ma dodatnie rozwiązanie? |
| 3x−m | | mx−4 | |
10 kwi 15:47
bezendu:
1. α=30
0
| | x2−5x+4 | | x2−5x+4 | |
3. |
| ≥1 lub |
| ≤−1 |
| | x2−1 | | x2−4 | |
10 kwi 18:34
Mila:
2) Popraw
3) dalej...
10 kwi 18:39
10 kwi 18:42
bezendu:
| | 9 | | 20 | |
Ostatnie to m∊( |
| , |
| )/{2√3} |
| | 5 | | 3 | |
Mam trochę problem z 3 b) ?
10 kwi 18:45
Piotr 10: w b) pozwijaj we wzory skrocnego mnozenia
10 kwi 18:47
Mila:
4) dobrze.
3) (a) przenosisz wszystko na jedna strone , sprowadasz do wspólnego mianownika , ...
| | x−1 | |
b) robisz podstawienie | |
| |=t, t≥0 |
| | x−2 | |
10 kwi 18:49
bezendu:
3. a
D=R\{−2,2}
(−5x+8)(x−2)(x+2)≥0
x(2x−5)(x−2)(x+2)≤0
I teraz część wspólna ale nie chcę mi się już jej wyznaczać
10 kwi 18:53
bezendu:
Mila ja wiem jak się rozwiązuję tylko miałem problem z tym b )
10 kwi 18:54
Mila:
3a − błąd w odpowiedzi, ma być suma zbiorów .
10 kwi 20:21
bezendu:
No to suma, przepraszam, źle spojrzałem na spójnik. Jednak upieram się na zadania z
planimetrii.
10 kwi 20:22
zawodus: Zadanie
Trójkąt ABC jest równoboczny. Na przedłużeniu boku AB i na boku BC obieramy odpowiednio punkty
Q i P w ten sposób, że |CP|=|BQ|. Wykaż, że |AP|=|PQ|.
10 kwi 20:31
bezendu:
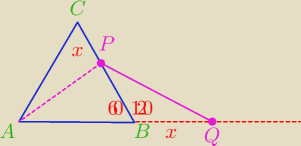
hmm ?
10 kwi 20:49
zawodus: Rysunek ok.
10 kwi 20:50
bezendu: A dalej?
10 kwi 21:02
zawodus: no czekamy na dowód

10 kwi 21:04
bezendu:
Z podobieństwa mam to zrobić ?
10 kwi 21:07
Mila:
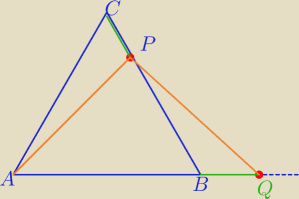
10 kwi 21:09
zawodus: wszystkie techniki dozwolone

10 kwi 21:09
bezendu:
Ale niestety mam tylko jeden bok taki sam, kąty raczej różne.
10 kwi 21:12
zawodus: bezendu To jest zadanie z podstawy, nie dostaniesz tak szybko wskazówki...

10 kwi 21:14
bezendu:
Masakra..
10 kwi 21:22
Mila:
Tw cosinusów, nie powiem, gdzie.
10 kwi 21:33
bezendu:
Tw cosinusów
d=AP
d2=a2+(a−x)2−2a*(a−x)*cos600 ?
10 kwi 21:38
Mila:
Dalej , PQ2=....
10 kwi 21:41
zawodus: i co dalej? wtedy?
popróbuj niech ci 3 razy nie wyjdzie to będziesz bardziej usatysfakcjonowany z uzyskania
rozwiązania

10 kwi 21:42
bezendu:
Ok i co teraz skoro mam PQ i AP ?
10 kwi 21:44
zawodus: Masz pokazać, że |PQ|=|AP|
10 kwi 21:45
bezendu:
To już mam, dzięki Mili, to było z podstawy ? Nie załamuj mnie !
10 kwi 21:54
Marcin: Twierdzenia cosinusów nie ma na podstawie o ile się nie mylę, ale co ja tam wiem, lecą na


Można prosić dowód bez twierdzenia?
10 kwi 21:55
bezendu:
Marcin przestań, bo brzuch Ci urośnie to się w garnitur nie zmieścisz na zakończenie

10 kwi 21:57
zawodus: No to próbujemy bez cosinusów

Ale proszę o robienie tylko przez maturzystów

10 kwi 21:58
Marcin: O to się nie boję. Na razie waga w normie

10 kwi 21:58
Marcin:
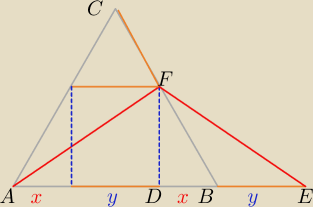
Byłoby ok?
10 kwi 22:21
zawodus: Ale co z tego wynika?
10 kwi 22:24
Marcin: ADF i DEF są identyczne więc AF= FE.
Nie będzie tak?

10 kwi 22:26
Marcin: Wybacz błąd oznaczeń.
10 kwi 22:29
zawodus: Ujdzie

10 kwi 22:33
Marcin: 

10 kwi 22:34
zawodus: Zapiszemy cię do grupy AA

11 kwi 07:37
Marcin: ok, ale idziesz ze mną

11 kwi 14:03
5-latek: Marcin ja spadam do pracy za chwile a TY lap
Na okregu o promieniu r opisano trapez rownoramienny
Punkt stycznosci dzieli ramie trapezu na odcinki ktorych dlugosci sa w stosunku 1:2. Oblicz
dlugosc promienia okregu opisanego na tym trapezie . Powodzenia >
11 kwi 14:08
Marcin: Dzięki za zadanko

11 kwi 14:33
zawodus: Ja?

Ja to chcę do więzienia i żebym mógł sobie książki z matmy pożyczać i inne też to by było moje
marzenie

i jeszcze net do forum

11 kwi 14:40
Marcin: Co do więzienia i książek z matmy, to chyba nie byłoby aż tak wielkiego problemu. Z internetem
z gorzej, ale nie można mieć przecież wszystkiego

11 kwi 14:51
zawodus: Ja muszę mieć wszystko

11 kwi 14:54
Marcin: Marzenia trzeba realizować stopniowo

Najpierw dostań się do więzienia

11 kwi 14:55
zawodus: Z tym to nie problem

Ostatnio mandat złapałem za przejście dla pieszych...
11 kwi 14:59
Marcin: Też dostałem. W dniu urodzin

Za to do wiezień nie wsadzają

11 kwi 15:00
zawodus: "Ci" ludzie są do bani spieszyłem się na ostatni autobus (następny za 3,5h). Nic nie jechało a
ten "uprzejmy człowiek" nic żadnego upomnienia tylko mandat...
Jakbym mu "podziękował" to bym trafił

11 kwi 15:01
Marcin: Następnym razem uciekaj

11 kwi 15:02
zawodus: Tak, myślisz, że to skutkuje?

11 kwi 15:14
Marcin: No pewnie

Sam muszę kiedyś spróbować

11 kwi 16:07
bezendu:
Czy tylko mi się tak, wydaję czy zadania na maturze R z planimetrii są takie proste ? Nie
chodzi o dowód.
11 kwi 19:49
Marcin: To zależy dla kogo. To co dla Ciebie jest banalne, dla mnie może być nie do zrobienia

11 kwi 19:54
bezendu:
Popatrz na zadania z matur 2010−2013 dotyczące planimetrii. Wydają się bardzo proste...
11 kwi 19:55
Draghan: Jak sobie przejrzysz matury, to w sumie tam nie ma wielu trudnych zadań w ogóle

Tylko właśnie dowody są trudne. A jak masz 2 lub 3 takie zadanka...

11 kwi 19:55
bezendu:
Czyli mam nadzieję, że jednak zrobię cały arkusz od A do Z !

11 kwi 19:57
Draghan: Czego Tobie, reszcie maturzystów (i sobie) życzę

Chociaż wiem, że ja wszystkiego nie zrobię

Ale trzeba być dobrej myśli

11 kwi 20:00
Marcin: Te z CKE nie są może jakichś najwyższych lotów

11 kwi 20:01
Marcin: Ja się będę cieszyć z każdego wyniku

11 kwi 20:02
bezendu: Ciężą tylko najwyższe noty !

11 kwi 20:02
Marcin: Oj tam przesadzasz

Czasem stres może Ci zepsuć kilka lat nauki

11 kwi 20:03
Piotr 10: Bez strachu

11 kwi 20:06
Draghan: Wiecie co?

Fajnie jest tak pogadać, ale...
DO ROBOTY! 

11 kwi 20:07
Marcin: Ty może tak. Ja w sumie też (piwko przed maturką


) ale nie każdy

11 kwi 20:08
5-latek: Marcin ale zacznij je robic
11 kwi 23:20
Marcin: Zadania? Tego od Ciebie jeszcze nie robiłem, bo jechałem z arkuszami. Jutro, dobrze?

11 kwi 23:43
Draghan: Jedno z zadań, podanych przez [Ż[Milę]], brzmi: Stosunek pola rombu do pola koła wpisanego w
ten romb wynosi 8:π. Oblicz miarę kąta ostrego tego rombu.
Prawidłowa odpowiedź to 30
o
| | 1 | |
A mi cały czas wychodzi sinα = |
| ≈ 0.05  |
| | 2π2 | |
Mógłby ktoś podrzucić małą (ale tylko małą

) wskazówkę, jak należy rozwiązać?
13 kwi 22:53
Draghan: Milę*
13 kwi 22:53
Mila:
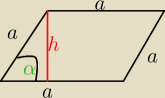
P
▱=a
2sinα
13 kwi 22:57
Draghan: Ech. Ja to liczyłem z
P=ah
i P=a
2sinα
Z tego policzyłem i z wiadomości o stosunku pól policzyłem a i później podstawiłem.
Dlaczego tak nie można?

13 kwi 23:02
13 kwi 23:24
Draghan: Mam teraz mały rebus



Rozwiązanie: ten z młotkiem, to ja

A ten obok, to też ja

Strzelający do samego siebie

Za głupotę.
Za każdym z pięciu razów, jak to liczyłem, liczyłem poprawnie

Tylko że w poleceniu jest
| | 8 | |
stosunek, wynoszący |
| . A ja za każdym razem podstawiałem 8*π. Bo nie widziałem tego |
| | π | |
dwukropka tam


Przepraszam, wczoraj mi się internet rozłączył, więc nie mogłem odpisać.
Dziękuję Ci,
Milu, za poświęcony czas


14 kwi 09:10
Draghan: A w
3b Jakie jest prawidłowe rozwiązanie nierówności
| | x2 − 2x + 1 | | x−1 | |
| |
| | + | |
| | − 12 < 0 ? |
| | x2 − 4x + 4 | | x−2 | |
Wyżej nie zauważyłem, żeby była wspomniana odpowiedź do tego zadania

Mój wynik to x ∊ (−oo;2) u (2.5;+oo). Czy jakaś dobra dusza mogłaby zweryfikować?

14 kwi 11:13
pigor: ..., no nie wiem, bo dla mnie ta nierówność przy
x≠2
sprowadza się np.do postaci
|x−1|< 3|x−2| ⇔ x
2−2x+1< 9x
2−36x+12 ⇔
8x2−34x+11 >0,
a tu nieciekawy trójmian o nieciekawej "delcie",...

14 kwi 11:42
Draghan: Hm
 x ≠ 2
x ≠ 2
| | x2 − 2x +1 | | x−1 | | (x−1)2 | | x−1 | |
| |
| | + | |
| | −12 < 0 ⇔| |
| | + | |
| |<12 |
| | x2 −4x +4 | | x−2 | | (x−2)2 | | x−2 | |
1.
| (x−1)2 | | x−1 | |
| + |
| < 12 |
| (x−2)2 | | x−2 | |
do wspólnego mianownika...
wymnożenie przez mianownik, później przeniesienie wszystkiego na lewo i wymnożenie...
−10x
2+43x−45 < 0
| | 5 | |
stąd x ∊ (−oo;2)u( |
| ;+oo) |
| | 2 | |
2.
| (x−1)2 | | x−1 | |
| + |
| > −12 |
| (x−2)2 | | x−2 | |
(...) brak miejsc zerowych, parabola leży nad osią OX, więc x ∊ R

14 kwi 12:01
Mila:
Wykonaj podstawienie:
Wtedy :
t
2+t−12<0
Δ=..
t∊(0,3)
|x−1|<3|x−2| i x ≠2 ⇔
(x−1)
2<9*(x−2)
2
dokończ.
14 kwi 12:07
Draghan: Dziękuję stukrotnie



Już nie mam siły analizować, co w tamtym skopałem

Źle ze mną chyba − śnią mi się zadania po
nocach

Ale jeszcze raz przeliczę, dla pewności

14 kwi 12:31
Mila:
Idź na spacer.

14 kwi 15:02
Marcin: Mi się jeszcze nigdy nie śniło zadanie

14 kwi 15:08
zawodus: Mnie się rozwiązania zadań których nie umiem śnią

14 kwi 16:25
Draghan: Dzięki

Właśnie ze spaceru wróciłem

Dwie godzinki

Nawet
miła pogoda

Mi się ostatnio dwa razy śniło

Raz to z prawdopodobieństwem, co prosiłem o potwierdzenie, a
Jeeny, wczoraj cały wieczór robiłem to zadanie z rombem i stosunkiem pól, na różne sposoby

I
cały czas wychodziło to samo, że α ≈ 3
o 
Już nawet zacząłem myśleć, że tablice mam jakieś
fałszywe

14 kwi 16:28
 Jeszcze raz inny sposób:
1) Znaleźć długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o
przyprostokątnych
a i b.
Jeszcze raz inny sposób:
1) Znaleźć długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o
przyprostokątnych
a i b.
 |AB|2=a2+b2+ab
|AB|2=ab(a+b)
|AB|=√ab(a+b)
Czy to jest ok do tej pory ?
|AB|2=a2+b2+ab
|AB|2=ab(a+b)
|AB|=√ab(a+b)
Czy to jest ok do tej pory ?





 Na kartce wyszło, tutaj nie koniecznie
Na kartce wyszło, tutaj nie koniecznie

 Dobranoc.
Dobranoc.
 hmm ?
hmm ?






 Można prosić dowód bez twierdzenia?
Można prosić dowód bez twierdzenia?

 Ale proszę o robienie tylko przez maturzystów
Ale proszę o robienie tylko przez maturzystów 

 Byłoby ok?
Byłoby ok?







 Ja to chcę do więzienia i żebym mógł sobie książki z matmy pożyczać i inne też to by było moje
marzenie
Ja to chcę do więzienia i żebym mógł sobie książki z matmy pożyczać i inne też to by było moje
marzenie  i jeszcze net do forum
i jeszcze net do forum 


 Najpierw dostań się do więzienia
Najpierw dostań się do więzienia 
 Ostatnio mandat złapałem za przejście dla pieszych...
Ostatnio mandat złapałem za przejście dla pieszych...
 Za to do wiezień nie wsadzają
Za to do wiezień nie wsadzają 



 Sam muszę kiedyś spróbować
Sam muszę kiedyś spróbować 

 Tylko właśnie dowody są trudne. A jak masz 2 lub 3 takie zadanka...
Tylko właśnie dowody są trudne. A jak masz 2 lub 3 takie zadanka... 

 Chociaż wiem, że ja wszystkiego nie zrobię
Chociaż wiem, że ja wszystkiego nie zrobię
 Ale trzeba być dobrej myśli
Ale trzeba być dobrej myśli 



 Czasem stres może Ci zepsuć kilka lat nauki
Czasem stres może Ci zepsuć kilka lat nauki 

 Fajnie jest tak pogadać, ale...
DO ROBOTY!
Fajnie jest tak pogadać, ale...
DO ROBOTY! 


 ) ale nie każdy
) ale nie każdy 


 ) wskazówkę, jak należy rozwiązać?
) wskazówkę, jak należy rozwiązać?
 P▱=a2sinα
P▱=a2sinα



 Rozwiązanie: ten z młotkiem, to ja
Rozwiązanie: ten z młotkiem, to ja  A ten obok, to też ja
A ten obok, to też ja  Strzelający do samego siebie
Strzelający do samego siebie  Za głupotę.
Za każdym z pięciu razów, jak to liczyłem, liczyłem poprawnie
Za głupotę.
Za każdym z pięciu razów, jak to liczyłem, liczyłem poprawnie  Tylko że w poleceniu jest
Tylko że w poleceniu jest

 Przepraszam, wczoraj mi się internet rozłączył, więc nie mogłem odpisać.
Dziękuję Ci, Milu, za poświęcony czas
Przepraszam, wczoraj mi się internet rozłączył, więc nie mogłem odpisać.
Dziękuję Ci, Milu, za poświęcony czas 

 Mój wynik to x ∊ (−oo;2) u (2.5;+oo). Czy jakaś dobra dusza mogłaby zweryfikować?
Mój wynik to x ∊ (−oo;2) u (2.5;+oo). Czy jakaś dobra dusza mogłaby zweryfikować? 

 x ≠ 2
x ≠ 2



 Już nie mam siły analizować, co w tamtym skopałem
Już nie mam siły analizować, co w tamtym skopałem  Źle ze mną chyba − śnią mi się zadania po
nocach
Źle ze mną chyba − śnią mi się zadania po
nocach  Ale jeszcze raz przeliczę, dla pewności
Ale jeszcze raz przeliczę, dla pewności 



 Właśnie ze spaceru wróciłem
Właśnie ze spaceru wróciłem  Dwie godzinki
Dwie godzinki  Nawet miła pogoda
Nawet miła pogoda  Mi się ostatnio dwa razy śniło
Mi się ostatnio dwa razy śniło  Raz to z prawdopodobieństwem, co prosiłem o potwierdzenie, a
Raz to z prawdopodobieństwem, co prosiłem o potwierdzenie, a
 I nie był to miły sen
I nie był to miły sen 

 I
cały czas wychodziło to samo, że α ≈ 3o
I
cały czas wychodziło to samo, że α ≈ 3o  Już nawet zacząłem myśleć, że tablice mam jakieś
fałszywe
Już nawet zacząłem myśleć, że tablice mam jakieś
fałszywe 