ehhh Nikt nie rozwiaze!: Pomóżcie mi z tym zadaniem, bo od 18 nikt nie potrafi tutaj mi go rozwiązać...... W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej ma długość 6. Kąt między przekątnymi dwóch sąsiednich ścian bocznych wychodzących z tego samego wierzchołka ma miarę 60stopni. Oblicz pole powierzchni graniastosłupa.

Tadeusz: ... chyba mylisz "formułę" tej strony. Nikt nie jest tu zobligowany do rozwiązywania ci zadań Pokaż co sam zrobiłeś ... próbowałeś ... Nawet rysunku nie zrobiłeś Psik ... psik ...

Nikt nie rozwiaze!: A czy ja mówię, że każę komuś to rozwiązać? Wyłącznie proszę o pomoc. A jeśli Ty nie masz ochoty jej udzielać to na co się spinasz...jeny.

jakubs: "bo od 18 nikt nie potrafi tutaj mi go rozwiązać......" Uwierz mi, że sporo osób potrafi. Odrobina chęci jakieś próby, rysunek czy cos...

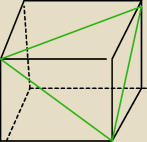
Draghan: Tak − mniej więcej − wygląda Twój graniastosłup. Zielona linia na ścianie bocznej ma długość 6. Po wykonaniu rysunku można zauważyć, że trójkąt, utworzony przez przekątne ścian bocznych, jest równoboczny (kąty 60 st.), co pociąga za sobą pewien fakt − graniastosłup ten jest sześcianem. Masz przekątną ściany bocznej sześcianu. Policzyć jego pole to pestka

J: Ja nie potrafię ... nie wiem jak inni.

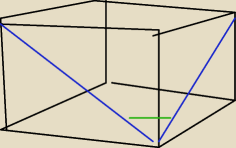
Nikt nie rozwiaze!: Kąt między przekątnymi dwóch sąsiednich ścian bocznych wychodzących z tego samego wierzchołka... nie wiem, czy to na pewno przekątne wychodzace z tego samego wierzchołka

Draghan: Hej, ludzie Spokojnie Niektórzy mają problem nawet ze sporządzeniem właściwego rysunku, ja sam ostatnio prosiłem o pomoc na forum (na moje nieszczęście − nie tym ), a okazało się, że przegapiłem mnożenie ułamków Luzik, nie trzeba się spinać Miłego wieczoru życzę

Nikt nie rozwiaze!: Do policzenia pola powierzchni szescianu potrzebuję długości boku a. Obliczę ten bok z trójkąta którego przeciwprostokątna ma miarę 6, bo jest rownoczesnie przekatna sciany bocznej, tylko, że....jak obliczyć do tego jedną z przyprostokątnych?

Draghan: Podpowiem jeszcze, że 6 to jednocześnie przekątna kwadratu Wgl mam nadzieję, że sam dobrze zinterpretowałem treść zadania Ja się za mocno na matmie nie znam

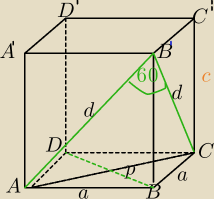
Mila: Tu trzeba się wykazać cierpliwością. Ktoś zawsze ( na ogół) rozwiąże. d=6 ΔACB' jest równoramienny o kącie między ramionami 60^o⇔że jest Δ równobocznym |AC|=6 p²=a²+a² 2a²=36 a²=18 a=√18 a=3√2 WΔB'C'C: c²+a²=d² c²=36−18 c=3√2 P_c=2*a²+4*a*c=2*18+4*3√2*3√2 P_c=36+36*2=36+72=108

Nikt nie rozwiaze!: czyli d=a√2

Nikt nie rozwiaze!: Dziękuje Ci Mila, dzisiaj ratujesz mi życie!

Mila: Staraj się sam więcej pracować, aby były korzyści z pomocy.

Draghan: Czyli dobrze zinterpretowałem! Fajnie wiedzieć I ja Tobie dziękuję, Mila

PW: Powiem tak: − Może i bym się postarał, ale jak widzę Twój prowokujący nick, to od razu omijam takie zadania. Skoro już wiesz ...

Mila: Witaj PW, też mnie irytują takie nicki, traktuję to jak lekceważenie.Też na ogół omijam. Myślę, że Nikt..., zmieni nicka od jutra i nam o tym napisze.

Filipo: Brzmi lepiej? Mimo tego, że za komputerem nadal siedzi ten sam człowiek...? Pozory mylą Panowie, chociaż ludzkość od zawsze się nimi kieruje.

Filipo: *I Panie.

PW:

Draghan: Pozory, pozorami, ale pierwsze wrażenie można zrobić tylko raz Później są tylko poprawki A ja mam jeszcze pytanie, ale niezwiązane z matematyką... Jeśli nie chcecie, nie odpowiadajcie, wiadomo PW i Milo, kim jesteście tak na co dzień? Wydajecie się być całkiem "fajnymi" ludźmi

PW: Pozory mylą (mówię o sobie)

Draghan: Nie przesadzajmy W końcu poświęcasz swój wolny czas, żeby pomóc innym I wykazujesz się przy tym niezbędną cierpliwością Nie możesz być aż taki niefajny Jesteś może nauczycielem? Czy studentem? Czy coś? Bo tłumaczysz zagadnienia bardzo dokładnie

Mila: Jestem Polak mały!

Eta:

Filipo: Nauczycielem raczej nie, bo zjechał metodę drzewek równo po bandzie i mówił o nauczycielach w 3 osobie.

5-latek: Nie zadzieraj z przewodniczacym wspolnoty mieszkaniowej Witam PW

Mila: Filip, rozwiązuj zadania. Zdajesz maturę? Kasztany mają juz liście.

Draghan: Metodę drzewek? ;__; Gdzie? ;__; Metoda drzewek jest spoko Oczywiście w wąskim zakresie zastosowań, bo jak masz dużo gałęzi, to można prędzej zgadnąć wynik, niż wyrysować dobre drzewo

Radek: Kasztany mają liście i co w związku z tym ?

Radek: Tzn, że już niczego się nie nauczę i te zadania co robię nic nie dadzą ?

5-latek: ja wlasnie wtedy zaczalen sie uczyc do matury

Draghan: W związku z tym maturzyści (czyli np. ja ) mają liczyć zadania, a nie wdawać się w zbędne i jałowe dyskusje Taka metafora − "kasztany mają liście, a Wy zadania liczcie" Ech, odbija mi już Idę spać Dobranoc

Filipo: A no tutaj: https://matematykaszkolna.pl/forum/245120.html Rozwiązuje zadania. Zdaję maturę. Kasztany mają już liście − oczywiście, wiem o tym. Ale pamiętaj, że trawa rodzi zielone owoce.

Draghan: Dobra, kapituluję Imć mistrz PW podważył mój światopogląd I rzeczywiście − odpowiedziałbym coś w stylu "tak to się rozwiązuje" Teraz tylko iść i płakać. A co to za jabłuszka takie fajne są na forum? Niosą za sobą jakieś ukryte znaczenie?

5-latek: Niektore moga byc robaczywki

Eta:

5-latek: Witam Eta

Draghan: Aha Dobrze wiedzieć Miło się rozmawiało, ale późno już. Idę płakać nad drzewkami (czyżby jabłonki? ) ;__; Dobrej nocy Do zobaczenia jutro