Rozwiązanie za pomocą drzewek.
Oskar: Z urny zawierającej kule różnych kolorów w tym 6 kul białych losujemy kolejno dwie kule bez
zwracania. Oblicz ile jest kul w urnie,jeżeli prawdopodobieństwo wylosowania dwóch kul tego
samego koloru jest równe 7/15.
3 kwi 23:02
PW: Zadanie jest sformułowane fatalnie. Co to znaczy „urna zawierająca kule różnych kolorów, w
tym 6 kul białych”? Tam są białe i jeszcze inne − np. czarne, czy też tych kolorów różnych od
białego może być kilka? Kule inne niż białe mogą występować po jednej, czy też co najmniej po
dwie?
Inny paskudny fragment treści zadania to „losujemy kolejno”. Sugestia, żeby uwzględniać w
modelu matematycznym kolejność losowanych kul, co wcale nie jest potrzebne do poprawnego
rozwiązania.
A już zupełnie nie rozumiem sugestii rozwiązania za pomocą drzewek. To ma być ułatwienie, czy
mącenie w głowach biednych uczniów?
4 kwi 17:44
marta:
"krzaki" .......ostatnio w szkołach są "modne"

4 kwi 19:42
Mila:
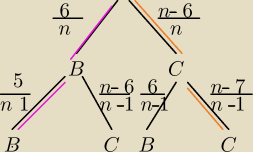
Jeżeli kule są w dwóch kolorach to tak:
n− liczba kul, n>6
6− liczba kul białych
n−6 liczba kul czarnych
A− wylosowano dwie kule białe (BB) lub dwie kule czarne (CC)
| | 6 | | 5 | | n−6 | | n−7 | | 7 | |
P(A)= |
| * |
| + |
| * |
| = |
| ⇔ |
| | n | | n−1 | | n | | n−1 | | 15 | |
| 30+n2−7n−6n+42 | | 7 | |
| = |
| |
| n*(n−1) | | 15 | |
15*(n
2−13n+72)=7*(n
2−n)
po rozwiązaniu:
4 kwi 20:07
PW: No i to właśnie mi się nie podoba. Drzewko to ... ukryty wzór Bayesa. Proste zadanie
zastępujemy skomplikowanym, w dodatku nie konstruując w sposób jawny modelu matematycznego.
W tym zadaniu model jest prosty: zdarzenia elementarne to 2−elementowe podzbiory zbioru
n−elementowego, n≥8.
Nie sugerujmy się określeniem "losujemy kolejno" − wynik losowania to dwie kule, nie nadajemy
im porządku, a więc losowanie polega na wyciągnięciu 2 kul spośród n.
Zdarzenie A − "wylosowano dwie kule tego samego koloru" jest sumą dwóch rozłącznych zdarzeń:
B − "wylosowano 2 kule białe"
C − "wylosowano dwie kule czarne".
| | | | | | 30 | | (n−6)(n−7) | |
|A| = |B| + |C| = | + | = |
| + |
| . |
| | | | 2 | | 2 | |
Z treści zadania wynika, że wylosowanie każdego dwuelementowego podzbioru jest jednakowo
prawdopodobne (spełnione są założenia twierdzenia zwanego klasyczną definicją
prawdopodobieństwa), zatem
| | |A| | | 30+(n−6)(n−7) | | n2 − 13n + 72 | |
P(A) = |
| = |
| = |
| . |
| | |Ω| | | n(n−1) | | n2−n | |
Dochodzimy do tego samego równania.
Nie trzeba nic rysować. Jasna jest konstrukcja przestrzeni Ω. Nie przemycamy w postaci gałązek
twierdzenia, którego uczeń pewnie jeszcze nie zna, a na pewno zapytany co robi odpowie "bo tak
się to rozwiązuje".
Moje wybrzydzanie odnosi się do "tendencji dydaktycznej" − jak to
marta mówi "mody na
krzaki", a nie do wiedzy
Mili, wobec której jestem malutki

.
4 kwi 21:54
Eta:

4 kwi 23:22

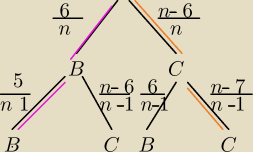 Jeżeli kule są w dwóch kolorach to tak:
n− liczba kul, n>6
6− liczba kul białych
n−6 liczba kul czarnych
A− wylosowano dwie kule białe (BB) lub dwie kule czarne (CC)
Jeżeli kule są w dwóch kolorach to tak:
n− liczba kul, n>6
6− liczba kul białych
n−6 liczba kul czarnych
A− wylosowano dwie kule białe (BB) lub dwie kule czarne (CC)
 .
.
