a
qu:

Z punktu A= (5,0) poprowadzona styczne do okręgu o równaniu x
2+y
2=4. Wyznacz tangens kąta,
pod którym przecinają sie te styczne
Tak bd wyglądał wysunek ? r=2 przechodzi przez początek układu ?
i co dalej ?
7 kwi 12:46
J: | | 2 | | 2tg(0.5α) | |
tg(0.5α) = |
| i tgα = |
| |
| | 5 | | 1 − tg2(0.5α) | |
7 kwi 12:52
qu: pierwsze rozumiem ale jak obliczyłeś to 2 ?
7 kwi 15:46
J: | | 2tgα | |
Ze wzoru : tg2α = |
| |
| | 1 − tg2α | |
7 kwi 15:53
qu: to jest ten wzór tg(α+β)=
tylko zamiast β jest dw razy α ?
7 kwi 16:04
qu: i później jak z 1/2 α zrobić α
7 kwi 16:18
J: α = 2*(0.5α) − podstawisz do gotowego wzoru, który Ci napisałem(12:52)
7 kwi 16:21
qu: ten co podałeśto jest ten wzór tg(α+β)= tylko zamiast β jest dw razy α ?
7 kwi 16:27
J:
| | sin2x | | 2sinxcosx | |
Mozna go wyprowadzć tak: tg2x = |
| = |
| i po |
| | cos2x | | cos2x − sin2x | |
podzieleniu licznika i mianownika przez cos
2x dostaniesz to równanie.
7 kwi 16:29
7 kwi 16:29
pigor: ... , czy taką masz odp. tg2x=
417√21 
7 kwi 16:43
J: A skąd
pigor masz taki dziwny wynik ?

7 kwi 16:45
J: Wycofuję pytanie

.... nie przyjrzałem się rysunkowi

7 kwi 16:48
qu: dobra mam ten wzór, wyszedł tak jak mówiłeś
teraz mam do niego podstawić tgα
lecz mam tg 1/2α
jak dodam 1/2+1/2 α to wyjdzie mi α ?
7 kwi 16:57
pigor: ..., no właśnie sam się dziwię, że taki nieciekawy

bo
pomyślałem tak:
niech a −odległość punktu A od punktu styczności , to
a
2= 3*(3+4) z tw. o stycznej i siecznej y=0 z punktu (5,0), stąd a=
√21
| | 2 | | 2 | |
zatem jeśli x miara kąta tej stycznej z OX to tgx= |
| = |
| √21 |
| | √21 | | 21 | |
czyli
| | 2tgx | | 2*221√21 | |
tg2x= |
| = |
| = |
| | 1−tg2x | | 1−421 | |
i co dobrze gadam, czy jakieś bzdety

sam zaczynam już wątpić .
7 kwi 17:01
J:
Nie, zadanie trzeba zacząć od poczatku, bo styczna nie przecina osi OY w punkcie (0,2) ..

Zasugerowałem sie rysunkiem ... bezpodstawnie

Na poczatek trzeba wyznaczyć punkt A , w którym styczna przecina os OY , potem sposób
postepowania będzie analogiczny
7 kwi 17:01
qu: wynik masz dobry

7 kwi 17:02
qu:
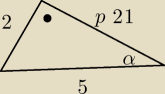
mi wychodzi taki trójkąt
2 bo promień okręgu
i jest pod kątem prostym do stycznej
7 kwi 17:04
J:
A nie można prościej .. niech Twoje a to odległość do punktu stycznośći...
mamy: a
2 + r
2 = 5
2 ..
| | r | |
albo jeszcze prościej , bez a ... |
| = sin(0.5α).. ? |
| | 5 | |
7 kwi 17:07
qu: i potem sinus jakoś zamienić na tangens ?
Nurtuje mnie jak z sin 1/2α zrobić sinα
7 kwi 17:09
J: | | 2 | |
OK,...czyli tg(0.5α) = |
| i dalej już tak samo. |
| | √21 | |
7 kwi 17:10
J: | | 2 | |
Nie trzeba, patrz na rysunek tg(0.5α) = |
| |
| | √21 | |
7 kwi 17:11
qu: właśnie do tego momentu mam i teraz żeby podstawić do wzoru muszę mieć cały tangens a mam
połowę i jak zrobić teraz cały ?
7 kwi 17:11
pigor: ..., np. tak :sinα= 2sin12α*cos12α= 2sin12α*√1−sin212α .
7 kwi 17:12
J: Idz do wzoru 12:52 i podstaw za tg(0.5α) i obliczysz tgα ... i PO ZADANIU !
7 kwi 17:13
J: Ale nie trzeba w to mieszać sinusa...
7 kwi 17:14
qu:
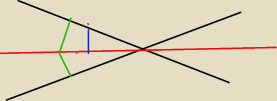
czyli mam niebieski kąt a szukam zielonego tak ?
Czy ten niebiski to już bedzie ten któego szukam ?
7 kwi 17:14
pigor: ...,
| | 2tg12α | |
tgα= |
| = podstawiaj to swoje ... |
| | 1−tg212 | |
7 kwi 17:15
J: Dałem mu ten wzór już w południe ..

7 kwi 17:15
J: Tak niebieski to kat 0.5α , a zielony (szukany0 to α
7 kwi 17:17
pigor: ..., no to szkoda szkoda czasu,
a co do mojego sposobu, to taki ...

wpadł
mi pierwszy i ...poszłoooo online. ...
7 kwi 17:20
 Z punktu A= (5,0) poprowadzona styczne do okręgu o równaniu x2+y2=4. Wyznacz tangens kąta,
pod którym przecinają sie te styczne
Tak bd wyglądał wysunek ? r=2 przechodzi przez początek układu ?
i co dalej ?
Z punktu A= (5,0) poprowadzona styczne do okręgu o równaniu x2+y2=4. Wyznacz tangens kąta,
pod którym przecinają sie te styczne
Tak bd wyglądał wysunek ? r=2 przechodzi przez początek układu ?
i co dalej ?


 .... nie przyjrzałem się rysunkowi
.... nie przyjrzałem się rysunkowi 
 bo
pomyślałem tak:
niech a −odległość punktu A od punktu styczności , to
a2= 3*(3+4) z tw. o stycznej i siecznej y=0 z punktu (5,0), stąd a=√21
bo
pomyślałem tak:
niech a −odległość punktu A od punktu styczności , to
a2= 3*(3+4) z tw. o stycznej i siecznej y=0 z punktu (5,0), stąd a=√21
 sam zaczynam już wątpić .
sam zaczynam już wątpić .
 Zasugerowałem sie rysunkiem ... bezpodstawnie
Zasugerowałem sie rysunkiem ... bezpodstawnie  Na poczatek trzeba wyznaczyć punkt A , w którym styczna przecina os OY , potem sposób
postepowania będzie analogiczny
Na poczatek trzeba wyznaczyć punkt A , w którym styczna przecina os OY , potem sposób
postepowania będzie analogiczny

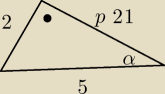 mi wychodzi taki trójkąt
2 bo promień okręgu
i jest pod kątem prostym do stycznej
mi wychodzi taki trójkąt
2 bo promień okręgu
i jest pod kątem prostym do stycznej
 czyli mam niebieski kąt a szukam zielonego tak ?
Czy ten niebiski to już bedzie ten któego szukam ?
czyli mam niebieski kąt a szukam zielonego tak ?
Czy ten niebiski to już bedzie ten któego szukam ?

 wpadł
mi pierwszy i ...poszłoooo online. ...
wpadł
mi pierwszy i ...poszłoooo online. ...