asd
Uczę się: Obrazem odcinka AB, gdzie a=(1,0) i B=(2,1) w jednokładkości o skali k>1 i środku P jest
odcinek CD, gdzie C=(4,0), D=(6,2).
Zapisz równanie okręgu o środku w punkcie P i promieniu |AB|
Co najpierw powinienem wyliczyć? Może odcinek AB z podanych dwóch punktów?
a ten środek w jak ten punkt obliczyć bo nawet jak czytam tą treść to nie kumam
6 kwi 20:55
6 kwi 20:59
Uczę się:
ale gdzie jest wgl ten punkt P?
6 kwi 21:04
Uczę się: pomoże ktoś?

6 kwi 21:40
Mila:
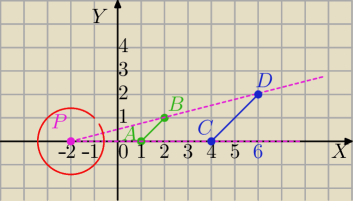
Właśnie masz wyznaczyc.
Najpierw skala :
|AB|=
√2
|CD|=2
√2
k>1 z założenia
k=2
Z definicji jednokładności:
k=2 skala, P(a,b) −środek jednokładności
A=(1,0) i B=(2,1)
C=(4,0), D=(6,2).
PC
→=2*PA
→⇔[4−a,0−b]=2*[1−a,0−b]
4−a=2−2a ⇔a=−2
−b=−2b⇔b=0
P=(−2,0) to można było odczytać z rysunku w tym zadaniu.
r=
√2
(x+2)
2+y
2=2 równanie okręgu
6 kwi 21:52
Uczę się: dziękuję baardzo

6 kwi 21:59
Mila: 
6 kwi 22:11
Uczę się: a jest gdzieś na matematyka.pisz o tej definicji jednokładności?
6 kwi 22:15
6 kwi 22:16
Uczę się: dzięki poraz kolejny xd
6 kwi 22:18
6 kwi 22:20
 ale gdzie jest wgl ten punkt P?
ale gdzie jest wgl ten punkt P?

 Właśnie masz wyznaczyc.
Najpierw skala :
|AB|=√2
|CD|=2√2
k>1 z założenia
Właśnie masz wyznaczyc.
Najpierw skala :
|AB|=√2
|CD|=2√2
k>1 z założenia

