??? Damo93: Narysuj wykres funkcji, która każdej wartości m, dla której istnieje trójkąt o wierzchołkach A=(m,2) B=(0,3) C=(5,m − 3) , przyporządkowuje pole tego trójkąta. Dla jakich wartości m pole trójkąta ABC jest równe 2.

	1
1. korzystam z wzoru na pole trójkąta : P =		I (Xb−Xa)(Yc−Ya) − (Yb − Ya)(Xc − Xa) I
	2

więc :

	1
P =		I −m2 +6m − 5I
	2

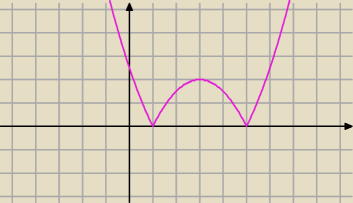
teraz z Δ wiem że dla me ∊ <2,4> wartość ≥0 a dla m ∊(−∞, 2) v (4, +∞) < 0 i co dalej teraz mam rysować te wykresy :

	1		5
f(m) = −		m2 + 3m −		dla m ∊ <2,4>
	2		2

	1		5
f(m) =		m2 − 3m +		dla m ∊ (−∞,2) v (4, +∞)
	2		2

Coś nie bardzo mi się to podoba, chyb coś pokręciłem

bezendu: m=3 lub m−3−2√2 lub m=3+√2

	1
Ja robię to ze wzoru na pole tego z tablic z i mam wykres f(m)=		|m2−6m+5|
	2

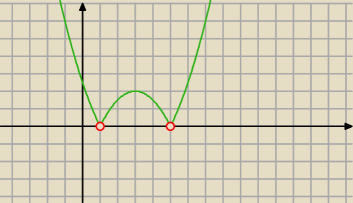
Godzio: m² − 6m + 5 m = 5 i m = 1 Ale tak się zastanawiam, nie musimy dorzucić warunków: a + b > c a + c > b b + c > a ?

Damo93: ok, czyli ogólnie dobrze myślałem dzięki.

bezendu: Trzeba, a ja zpomniałem

Damo93: Godzio: wydaje mi się że to już się samo z tego pola wyklucza

Godzio: I to znaczy, że dla każdego m istnieje trójkąt? Coś mi się wierzyć nie chce

Mila: m≠1 i m≠5 Wyjaśnienie pod adresem. https://matematykaszkolna.pl/forum/244444.html godzina 20:44