analityczna
Radek:
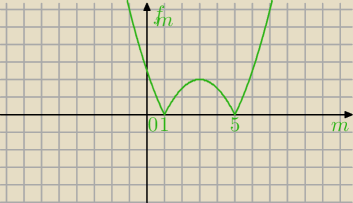
narysuj wykres funkcji która każdej wartości m, dla której istnieje trójkąt o wierzchołkach
A=(m,2)
B=(0,3) C=(5,m−3) przyporządkowuje jego pole tego trójkąta. Dla jakich wartości m pole tego
trójkąta ABC jest równe 2
Wiem jak zrobić drugą cześć polecenia nie wiem jak pierwszą
30 mar 21:27
zawodus: A jak liczysz pole?
To będzie funkcja pola.
Warto pamiętać, że wszystkie punkty nie mogą być współliniowe

30 mar 21:29
Radek:
| 1 | |
| |...| z tego wzoru z tablic |
| 2 | |
30 mar 21:30
Radek: ?
30 mar 21:34
zawodus: dobrze to to jest twoja funkcja P(m)=

30 mar 21:37
Radek:
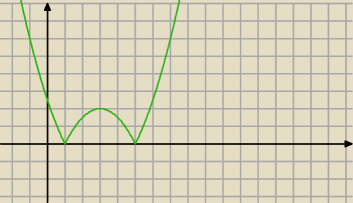
P=0,5|(0−m)(m−3−2)−(3−2)(5−m)|
P=0,5|(−m)(m−5)−(5−m)|
P=0,5|−m
2+5m−5+m|
P=0,5|−m
2+6m−5|
30 mar 21:40
Mila:
Jest sposób z zastosowaniem wektorów i wyznacznika.
Czy liczysz tak pole trójkąta, czy innego sposobu szukać?
30 mar 21:41
Radek: Z tego wzoru z tablic ze strony 6 (xb−xa)....
30 mar 21:42
Mila:
Dobrze, już widzę.Wzór z tablic.
Zastanów się jakie ograniczenia wprowadzić.
30 mar 21:42
zawodus: Nie mogę zrozumieć jak ty liczysz to pole.
Mila w karcie wzorów jest ten wzór bez wyznaczników.
(wg mnie trudniej zapamiętać), ale jak mają kartę to niech korzystają

30 mar 21:43
Radek:
Jeszcze trzeba coś wprowadzać ?
30 mar 21:43
zawodus: dobra wycofuje post

30 mar 21:44
zawodus: kiedy można utworzyć trójkąt?
pisałem ci u góry o warunku.
30 mar 21:44
Radek:
nie piałeś nic b<a+c i c<a+b a<a+b ?
30 mar 21:51
zawodus: bo tutaj to nie występuje − to jest analityczna.
Zobacz co napisałem wyżej.
30 mar 21:55
Radek:
Napisałeś funkcja i tyle.
30 mar 21:57
Mila:
Wzór na pole możesz zapisać tak:
| | 1 | |
P= |
| |m2−6m+5| wykres dobry |
| | 2 | |
Jakie nie może być m?
30 mar 21:59
Radek:
m∊<0,∞) ?
30 mar 22:03
Radek:
o to chodzi ?
30 mar 22:10
Mila:
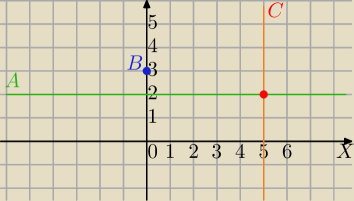
Jeszcze raz rysuję, tym razem warunki początkowe.
B=(0,3)
Nie powstanie Δ jeśli
A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
m≠.....
Nie powstanie Δ jeśli A,B,C będą współliniowe
y=ax+3
Próbuj dalej.
30 mar 22:19
Radek:
Czemu nie mogą skoro punky (5,2) nalezy do wykresu ?
30 mar 22:22
Mila:
Wtedy masz dwa wierzchołki, bo A pokrywa się z C i nie możesz narysować Δ.
Drugi zakaz
A,B,C leżą na jednej prostej.
y=ax+3, bo punkt (0,3) leży na prostej, której szukamy.
2=a*m+3
m−3=5a+3 wyznaczam m,
m=5a +6 podstawiam do pierwszego równania
a*(5a+6)+3=2
rozwiąż, napisz równania prostych.
30 mar 22:31
Radek:
Nadala nie rozumiem przejdę do innego zadania a do tego wrócę jutro bo jakoś wgl nie mogę
zrozumieć
30 mar 22:33
Mila:
Aby narysować trójkąt musisz mieć 3 różne punkty nie leżące na jednej prostej.
30 mar 22:51
Radek:
Tak, to rozumiem
30 mar 22:53
Radek:
Wyznacz równanie okręgu, który jest obrazem okręgu (x+4)
2+(y−7)
=27 w jednokładności o
| | 1 | |
środku S = (− 1,4) i skali |
| . |
| | 3 | |
Nie wiem jak robić takie coś ?
S
1=(−4,7) r=3
√3
30 mar 23:11
Radek:
?
30 mar 23:23
Mila:
S = (− 1,4) ,S1=(−4,7)
To chyba robiliśmy wektorowo, [czy umiesz wzór na współrzędne punktu po przekształceniu?]
S'
1(x',y')
| | 1 | |
[x'−(−1),y'−4]= |
| *[−4−(−1),7−4] |
| | 3 | |
x'+1=−1
y'−4=1
x'=−2
y'=5
S'
1=(−2,5), r=
√3
Pisz równanie nowego okręgu
30 mar 23:36
30 mar 23:38
Mila:
Dobrze, tak masz robić.
30 mar 23:40
Radek:
i tego nie mogę zrozumieć jak mam skalę i środek, Na odwrót umiem
30 mar 23:41
Radek: ?
31 mar 18:14
Mila:
Radek, przecież masz definicję.
Liczysz współrzędne wektorów: (od wsp. końca odejmujesz wsp. początku wektora )
SA i SA', gdzie S −środek jednokładności
A− punkt dany
A' −punkt szukany
SA'→=k*SA→ zgodnie z def. jednokładności.
31 mar 18:32
Radek: Dobrze, ale nie wychodzi mi i dlatego pytam.
31 mar 18:36
Radek:
Ma Pani jeszcze trochę czasu ?
31 mar 19:18
Mila:
23:30 napisałam jak zrobić, masz inne podobne zadanie to pisz.
31 mar 19:25
Radek:
Mam kilka zadań z jednokładności właśnie

Obrazem trójkąta ABC o wierzchołkach A = (1,3), B = (2 ,−3 ), C = (− 1,4) w jednokładności o
środku S = (2,1) i skali − 3 jest trójkąt KLM . Wyznacz współrzędne wierzchołków trójkąta
KLM .
Jak wyznaczyć skalę jeśli mam figurę ?
31 mar 19:30
Mila:
Skalę masz podaną , środek jednokładności też.
k=−3 ⇔figurę zwiększono 3 razy.
Licz wg wzoru:
x'=k(x−a)+a
y'=k(y−b)+b
a=2
b=1
k=−3
31 mar 19:48
Radek: K = (5,− 5), L = (2,13), M = (1 1,− 8) ?
31 mar 19:53
Mila:
Dobrze, liczyłeś wektorami, czy wg wzoru?
31 mar 19:59
Radek: wektorami.
31 mar 20:02
Mila:
No i pięknie.
31 mar 20:23
Radek:
Te arkusze z zielonego aksjomatu zrobiłem wszystkie przez niedzielę 11 arkuszy i wszystkie
zadanie bez wskazówek więc jest jakaś nadzieją na to skromne 80%
31 mar 20:28
Mila:
Pracuj dalej, bo studia przed Tobą.
31 mar 20:29
zawodus: Studia to " inna" matematyka.
31 mar 20:31
Radek:
Nie wiem czy pójdę w tym roku na studia, bo trochę sprawy osobiste i rodzinne mają na to wpływ.
31 mar 20:32
Radek: I dlatego chcę zdać maturę jak najlepiej w tym roku.
31 mar 20:34
Radek:
Końcami odcinka są punkty o współrzędnych A = (− 1,− 2) oraz B = (3,6) . Odcinek CD jest
obrazem odcinka AB zarówno w jednokładności o dodatniej skali i środku S1 = (− 5,2) , jak i w
jednokładności o ujemnej skali i środku S = (3,2) 2 . Oblicz współrzędne końców odcinka CD
oraz skalę jednokładności o środku S2 .
31 mar 20:35
Radek: ?
31 mar 20:54
Mila:
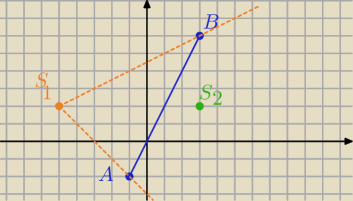
W jednokładności dodatniej o skali k>0
S
1C
→=k*S
1A
→ C(x
c,y
c)
S
1D
→=k*S
1B
→ D(x
d,y
d)
W jednokładności ujemnej o skali (−k), k>0
S
2C
→=−k*S
2B
→
S
2D
→=−k*S
2A
→
31 mar 21:15
Radek:
Też z tego wcześniejszego wzoru ?
31 mar 21:17
Mila:
Podałam Ci z definicji⇔wektorami, bo napisałeś, że poprzednie tak liczyłeś, ale wzory też mogą
być.
Wzorami łatwiej.
Tylko pamiętaj ,żeby punkty dać odwrotnie przy skali ujemnej ⇔obrazem punktu A jest D, obrazem
punktu B jest C.
31 mar 21:23
Radek:
To będę robił wzorem.
31 mar 21:25
Radek:
To teraz czas na bryły−stożek

31 mar 21:55
Radek:
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości
stożka do objętości walca wynosi 8:3. Oblicz tangens kąta zawartego między wysokością a
tworzącą stożka.?
31 mar 22:00
Mila:
Skończyłeś poprzednie zadanie? k=?, C, D
Co w tej bryłce jest niejasne?
31 mar 22:02
Radek:
C = (3,−6) , D = (1 1,10) , k = − 4 ?
31 mar 22:04
Radek:
8πr
12h
1=πr
2h2
8r
12r
2=πr
22h
2 ?
31 mar 22:12
Mila:
k=−2
31 mar 22:17
Mila:
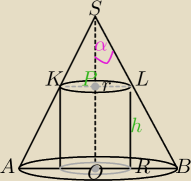
2) poupraszczaj.
Lepiej zapisz oznaczenia bez indeksów, (jeśli można), wtedy mniej okazji do pomyłek.
przez r
2 i π
r− promień walca
R− promień podstawy stożka
OS=H − wysokość stożka
h=R − wysokość walca
Dalej sam.
31 mar 22:27
Radek:
i co mam teraz wyznaczyć Wyznaczę sam tylko jaką literkę ?
31 mar 22:33
Radek: ?
31 mar 22:46
Mila:
wyznacz r i wstaw do Twojego wzoru po uproszczeniu.
Zauważ, że
31 mar 22:50
31 mar 22:52
Radek: A jeszcze czemu moje rozpisanie nie jest prawidłowe ?
31 mar 22:53
Mila:
Zapomniałes tam uprościć przez π, w pierwszej linijce obie wysokości oznaczyłeś tą samą literka
h.
31 mar 22:55
Radek:
8r12r2=r2h2 ?
Za h1 wstawiłem r2 z treści zadania
31 mar 23:03
Mila:
Tu znowu opuściłeś 3.
Napisz tgα według Twoich oznaczeń.
31 mar 23:08
Mila:
Radek, to zadanie jest bardzo nietypowe i wątpię, aby się takie pojawiło na maturze.
W dalszych rachunkach otrzymasz równanie 3 stopnia, po podstawieniu za tgα.
31 mar 23:14
Radek:
Ale warto zrobić te trudne zadania, nie wiadomo co może być a nie chcę mieć −10%
31 mar 23:16
Mila: rozwiąż.
1)Dlugość wysokości ostrosłupa prawidłowego trójkatnego jest równa długości krawędzi podstawy,
wyznacz miarę kąta między krawędzią boczną a płaszyzną podstawy.
2)) W ostrosłupie prawidlowym czworokątnym, krawędź podstawy ma długość a,
natomiast kąt między krawędzią boczną i krawedzią podstawy wychodzącą z tego samego
wierzcholka ma miarę α.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
31 mar 23:16
Mila:
To rozwiązuj tamto zadanie jak Ci podpowiadałam, nie mam nic przeciwko , ale lepiej się opanuje
materiał na innych zadaniach.
31 mar 23:17
31 mar 23:19
Radek:
1.α=600 ?
31 mar 23:30
Mila:
Dobrze (1)
31 mar 23:33
Mila:
3)
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy równej 2√3
i wysokości równej 3. Graniastosłup ten przecięto płaszczyzną zawierającą krawędź podstawy i
nachyloną do płaszczyzny podstawy pod kątem 30 stopni.
Oblicz pole otrzymanego przekroju. Narysuj ten przekrój.
31 mar 23:35
Radek: Teraz myślę nad drugim. Chcę sam zrobić tę zadania.
31 mar 23:38
Radek:
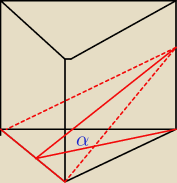
3.
pole przekroju 6 j
2 ?
1 kwi 12:08
Mila:
Dobrze.
1 kwi 17:18
Radek:
Na to drugie nie mam pomysłu, ale jeszcze spróbuje
1 kwi 17:32
Radek:
Mogła by mi Pani jeszcze raz wytłumaczyć to zadanie pierwsze w tym wątku z polem trójkąta ?
1 kwi 17:48
Radek: ?
1 kwi 18:07
Mila:
Z której godziny, tyle komentarzy więc nie wiem o co Ci chodzi.
1 kwi 18:11
Radek: 30 marca 22:19
wiem, że punkty nie mogą być współliniowe
1 kwi 18:14
Mila:
Za godzinę, bo będę teraz smażyć rybkę.
1 kwi 18:16
Radek: Dobrze poczekam, smacznego

1 kwi 18:21
Radek: ?
1 kwi 20:02
Mila:
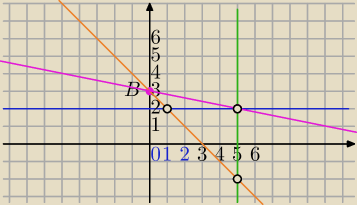
Narysuj wykres funkcji która każdej wartości m, dla której istnieje trójkąt o wierzchołkach
A=(m,2)
B=(0,3) C=(5,m−3) przyporządkowuje jego pole tego trójkąta. Dla jakich wartości m pole tego
trójkąta ABC jest równe 2.
1) zastanowimy się dla jakiego m nie może istnieć ΔABC
B=(0,3)
1)Nie powstanie Δ jeśli A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
A≠(5,2) C≠(5,2)⇔m≠5
2) Nie powstanie Δ jeśli A,B,C będą współliniowe⇔A,B,C leżą na jednej prostej
y=ax+3 wzór prostych przechodzących przez punkt B
3) Badamy dla jakich m wsp.punktów A i C spełniają równanie y=ax+3
2=a*m+3
m−3=5a+3 wyznaczam m,
m=5a +6 podstawiam do pierwszego równania
| | −1 | |
a*(5a+6)+3=2⇔a=−1 lub a= |
| |
| | 5 | |
Mamy dwie proste:
y=−x+3 wtedy m=1 i A=(1,2) oraz C=(5,−2)
| | 1 | |
y=− |
| x+3 , wtedy m=5 i A=(5,2) oraz C=(5,2) |
| | 5 | |
Wniosek :m≠5 i m≠1
rozwiążesz?
Czy masz odpowiedź do tego zadania?
Pozostaje wykres, ale najpierw mi daj odpowiedź.
Chcę ustalic dziedzinę funkcji.
1 kwi 20:44
Radek:
Ja wiem jak rozwiązać to równanie. Mam odpowiedź
tak jak Pani podała m≠{1,5}
1 kwi 20:58
Mila:
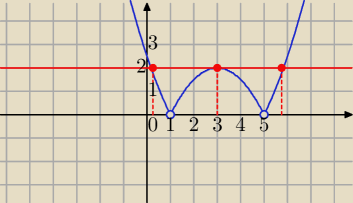
W takim razie co jeszcze mam wyjaśnić?
Otrzymałeś , że pole=2 dla
m=3−2
√2,
m=3+2
√2
m=3
1 kwi 21:03
Radek:
Mi chodzi o tą dziedzinę
1 kwi 21:04
Mila:
D=R\{1,5}
1 kwi 21:06
Radek: czyli trzeba pisać równania prostych tak i miejsca przecięcia wykluczyć ?
1 kwi 21:07
Radek: ?
1 kwi 21:21
Mila:
Opisałam dokładnie.
Wykluczasz punkty wspóliniowe.
1 kwi 21:23
Radek:
Dziękuję to jeszcze kilka zadań z tej analitycznej i stożek który wgl nie idzie
1 kwi 21:29
Mila:
Dawaj stożek.
Skąd miałeś to zadanko ostatnie?
1 kwi 21:32
Radek:
Arkusze maturalne wydawnictwo Aksjomat.
1 kwi 21:43
Radek: Stożek, którego pole powierzchni bocznej jest równe 9√10π , jest wpisany w kulę o promieniu
5. Oblicz objętość stożka.
Proszę o rysunek.
1 kwi 21:45
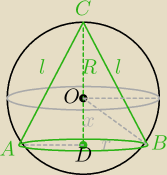
Mila:
1 kwi 22:00
Radek:
πrl=9√10π
rl=9√10
z podobieństwa ale nie wiem jak ?
1 kwi 22:06
Mila:
ΔABC jest wpisany w okrąg o promieniu R=5
|AB|=2r stąd
Teraz oblicz pole Δ na dwa sposoby i oblicz h=|CD|.
1 kwi 22:25
Radek:
skąd taki sin?
1 kwi 22:27
1 kwi 22:36
Radek:
P=0,5*sinC*l*l ?
1 kwi 22:40
Mila:
potem
| | 1 | |
PΔ= |
| *2r*h=0,5*sinC*l*l ⇔ |
| | 2 | |
oblicz h i wstaw do wzoru na V
stożka
1 kwi 22:44
Radek:
Ale czemu te pola są przyrównywane ?
1 kwi 22:44
Mila:
Zrób to, co Ci podpowiedziałam.22:44
1 kwi 22:54
Radek:
Nie chcę robić czego ,,ślepo,, czego nie rozumiem.
1 kwi 22:57
Mila:
Porównujesz, aby obliczyć h potrzebne do obliczenia objętości. Ponadto musisz wykorzystać
związek r*l=9√10, bo nic innego nie masz .
Są różne sposoby rozwiązywania.
Jeśli masz inną koncepcję, to ją włącz.
W geometrii często wykorzystuje się porównywanie pola Δ obliczonego dwoma sposobami.
1 kwi 23:06
Radek:
rl=9√10 z tego wyznaczyć l i policzyć pole z tego wozru ze sinusem
1 kwi 23:08
Mila:
Nie , wyznaczyc najpierw h z porównania pól.22:44
1 kwi 23:09
Radek: ok
1 kwi 23:13
bezendu:
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości
stożka do objętości walca wynosi 8:3. Oblicz tangens kąta zawartego między wysokością a
tworzącą stożka.?
Przepraszam, że się wtrącam ale wracając do tego zadania czy nie może być tak proporcja ?
1 kwi 23:15
Mila:
No to jak tam dokończyłeś?
Bezendu moze być, trzeba pisać, jakie Δ bierze się pod uwagę.
Ja wzięłam mały górny i duży, a Ty mały boczny i duży, to jest prawidłowe, dobrze, że zaczynasz
to widzieć.
1 kwi 23:23
bezendu:
Ciekawe zadanie, więc robię sobie wszystkie jakie są na forum. Tylko nie wstawiam swoich
wersji. Dziękuję za odp

1 kwi 23:25
Radek:
Nie dokończyłem jeszcze.
1 kwi 23:26
Radek: 27π
1 kwi 23:33
Mila:
Mnie wyszło tak:
| | 1 | | 1 | | l2 | | 1 | | 1 | |
V= |
| πr2*h= |
| π*r2* |
| = |
| π*(r*l)2= |
| π*(9√10)2= |
| | 3 | | 3 | | 10 | | 30 | | 30 | |
1 kwi 23:43
Mila:
Dobranoc.
1 kwi 23:43
Radek:
Dobranoc. Dziękuję za pomoc

1 kwi 23:46


 P=0,5|(0−m)(m−3−2)−(3−2)(5−m)|
P=0,5|(−m)(m−5)−(5−m)|
P=0,5|−m2+5m−5+m|
P=0,5|−m2+6m−5|
P=0,5|(0−m)(m−3−2)−(3−2)(5−m)|
P=0,5|(−m)(m−5)−(5−m)|
P=0,5|−m2+5m−5+m|
P=0,5|−m2+6m−5|


 Wzór na pole możesz zapisać tak:
Wzór na pole możesz zapisać tak:
 Jeszcze raz rysuję, tym razem warunki początkowe.
B=(0,3)
Nie powstanie Δ jeśli A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
m≠.....
Nie powstanie Δ jeśli A,B,C będą współliniowe
y=ax+3
Próbuj dalej.
Jeszcze raz rysuję, tym razem warunki początkowe.
B=(0,3)
Nie powstanie Δ jeśli A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
m≠.....
Nie powstanie Δ jeśli A,B,C będą współliniowe
y=ax+3
Próbuj dalej.
 Obrazem trójkąta ABC o wierzchołkach A = (1,3), B = (2 ,−3 ), C = (− 1,4) w jednokładności o
środku S = (2,1) i skali − 3 jest trójkąt KLM . Wyznacz współrzędne wierzchołków trójkąta
KLM .
Jak wyznaczyć skalę jeśli mam figurę ?
Obrazem trójkąta ABC o wierzchołkach A = (1,3), B = (2 ,−3 ), C = (− 1,4) w jednokładności o
środku S = (2,1) i skali − 3 jest trójkąt KLM . Wyznacz współrzędne wierzchołków trójkąta
KLM .
Jak wyznaczyć skalę jeśli mam figurę ?
 W jednokładności dodatniej o skali k>0
S1C→=k*S1A→ C(xc,yc)
S1D→=k*S1B→ D(xd,yd)
W jednokładności ujemnej o skali (−k), k>0
S2C→=−k*S2B→
S2D→=−k*S2A→
W jednokładności dodatniej o skali k>0
S1C→=k*S1A→ C(xc,yc)
S1D→=k*S1B→ D(xd,yd)
W jednokładności ujemnej o skali (−k), k>0
S2C→=−k*S2B→
S2D→=−k*S2A→

 2) poupraszczaj.
Lepiej zapisz oznaczenia bez indeksów, (jeśli można), wtedy mniej okazji do pomyłek.
przez r2 i π
r− promień walca
R− promień podstawy stożka
OS=H − wysokość stożka
h=R − wysokość walca
2) poupraszczaj.
Lepiej zapisz oznaczenia bez indeksów, (jeśli można), wtedy mniej okazji do pomyłek.
przez r2 i π
r− promień walca
R− promień podstawy stożka
OS=H − wysokość stożka
h=R − wysokość walca
 3.
pole przekroju 6 j2 ?
3.
pole przekroju 6 j2 ?

 Narysuj wykres funkcji która każdej wartości m, dla której istnieje trójkąt o wierzchołkach
A=(m,2)
B=(0,3) C=(5,m−3) przyporządkowuje jego pole tego trójkąta. Dla jakich wartości m pole tego
trójkąta ABC jest równe 2.
1) zastanowimy się dla jakiego m nie może istnieć ΔABC
B=(0,3)
1)Nie powstanie Δ jeśli A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
A≠(5,2) C≠(5,2)⇔m≠5
2) Nie powstanie Δ jeśli A,B,C będą współliniowe⇔A,B,C leżą na jednej prostej
y=ax+3 wzór prostych przechodzących przez punkt B
3) Badamy dla jakich m wsp.punktów A i C spełniają równanie y=ax+3
2=a*m+3
m−3=5a+3 wyznaczam m,
m=5a +6 podstawiam do pierwszego równania
Narysuj wykres funkcji która każdej wartości m, dla której istnieje trójkąt o wierzchołkach
A=(m,2)
B=(0,3) C=(5,m−3) przyporządkowuje jego pole tego trójkąta. Dla jakich wartości m pole tego
trójkąta ABC jest równe 2.
1) zastanowimy się dla jakiego m nie może istnieć ΔABC
B=(0,3)
1)Nie powstanie Δ jeśli A=C , nie mogą się znaleźć na skrzyżowaniu prostych x=5 i y=2.⇔
A≠(5,2) C≠(5,2)⇔m≠5
2) Nie powstanie Δ jeśli A,B,C będą współliniowe⇔A,B,C leżą na jednej prostej
y=ax+3 wzór prostych przechodzących przez punkt B
3) Badamy dla jakich m wsp.punktów A i C spełniają równanie y=ax+3
2=a*m+3
m−3=5a+3 wyznaczam m,
m=5a +6 podstawiam do pierwszego równania
 W takim razie co jeszcze mam wyjaśnić?
Otrzymałeś , że pole=2 dla
m=3−2√2,
m=3+2√2
m=3
W takim razie co jeszcze mam wyjaśnić?
Otrzymałeś , że pole=2 dla
m=3−2√2,
m=3+2√2
m=3


