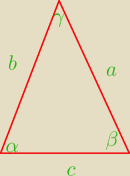
. Piotr 10: Wykaż, że jeśli α,β,γ są kątami wewnętrznymi trójkąta i sin²α+sin²β=5sin²γ, to

	3
sinγ ≤		.
	5

z tw. sinusów

2
	=2R , zatem korzystając z równania
sinα

a2		b2		c2
	+		= 5*
4R2		4R2		4R2

a²+b²=5c² z tw. kosinusów wyznaczam cosγ c²=a²+b² −2abcosγ

	2a2+2b2
cosγ=
	5ab

sin²γ+cos²γ=1 i z wyliczenia mam, ze

	√17(ab)2 − 4(a4+b4)
sinγ=
	5ab

i nie wiem co dalej zbytnio

pomocnik: Ale to już było i ... https://matematykaszkolna.pl/forum/244317.html

Piotr 10: A no tak, Dzięki wielkie

pomocnik: To nie moja zasługa tylko PW. pozdr.

pigor: ..., lub , aby pociągnąć to na czym skończyłeś : (a²−b²)² ≥ 0 ⇔ a⁴+b⁴ ≥ 2a²b² /*(−4) ⇔ −4(a²+b²) ≤ 8a²b² a więc ze swojej równości masz :

	√17a2b2−8a2b2		√9a2b2
sinγ ≤		=		=35 c.n.w.
	5ab		5ab

Piotr 10: ok thx