bryły bezendu: bryły W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 2α . Wyznacz objętość tego ostrosłupa Wracam do tego zadania, bo już dwa razy mnie ''powaliło''

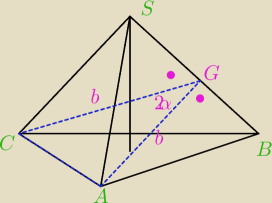
bezendu: 1. Mogę wyznaczyć b w zależności od a ?

Saizou : możesz

	1   a 2
sinα=
	b

bezendu: nie nie nie. a²=b²+b²−2b²cos2α a²=2b²−2b²cos2α a²=b²(2−2cos2α) a=b√2−2cosα

bezendu: Co teraz mogę wyznaczyć ?

Mila: Ważne , co chcesz dalej liczyc po kolei. ( sposoby sa różne)

bezendu: Pp=(b√2−2cosα²√3}{4}

	(b2−b2cosα)√3
Pp=
	2

Mila: "a" masz dane, miałeś obliczyć b, opuściłeś pod pierwistkiem 2 w cosinusie.

Piotr 10: pokombiuj cos moze z przyrownaniem pól

Mila: Patrz na treść, liczysz pole, a w treści V.

bezendu:

	(b2−b2cos2α)√3
Pp=
	2

To jak przerobić, żeby mieć b w zależności od a ?

bezendu:

	a2√3
Pp=
	4

Teraz potrzebuje tylko wysokości

Piotr 10: Wyraz pole trojkata ASB dwoma sposobami , poźniej tw kos CGA

bezendu: Ale i tak będę miał nową zmienną ? Tak ? Nie chodzi mi, żeby ktoś rozwiązywał.

Piotr 10: no wlasnie o to chodzi wtedy z tw pitagorasa można wyliczyc H mając dlugosci ze zmienna a

bezendu: no i pięknie

Mila: 22:26 masz : a=b*√2−2cos(2α) /:(√2−2cos(2α)

	a
b=
	√2−2cos(2α)

Lepiej radził Saizou, prostsze wyrażenie. Oblicz sinus ∡ABS, potem krawędz boczną ,

bezendu: w porównaniu do tych obliczeń to to jest łatwa wersja. Bo tamte są bardzo skomplikowane https://matematykaszkolna.pl/forum/237014.html

zawodus: Główny cel − policzenie wysokości. Można się do niej "dobrać" na trzy sposoby (najbardziej popularne). 1. Wg mnie najkrótsza droga to policzenie wysokości przekroju, a potem raz Pitagoras i raz podobieństwo trójkątów. 2. Droga prowadząca do krawędzi bocznej, a potem wysokości −− wymaga większej liczby kroków. 3 Można jeszcze przez wysokość ściany bocznej −− też rachunki gorsze. Niekiedy nie da się ominąć paru ułamków i funkcji trygonometrycznych

bezendu: Ok, dziś po południu.