bryły
bezendu:
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość a . Ściany boczne są
trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa 2α .
Wyznacz objętość tego ostrosłupa
I dalej nie mam nic ?
11 lut 22:44
Bizon:
... masz wystarczająco dużo −
11 lut 22:50
bezendu:
11 lut 22:51
Saizou :
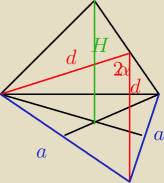
11 lut 22:56
Mila:
Sporo liczenia, jutro .
11 lut 22:57
bezendu:
Ja chyba też nie wpadnę na rozwiązanie.
11 lut 23:00
Saizou : nie jest takie trudne znowu
11 lut 23:01
bezendu: Dla mnie jest. Ale jutro to chyba dokończę.
11 lut 23:03
Bizon:
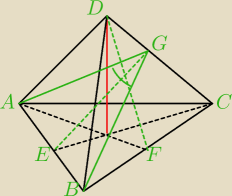
| |EB| | | a | |
| =sinα ⇒ |BG|= |
| |
| |BG| | | 2sinα | |
ΔBCG podobny do ΔFCD
... itd
12 lut 12:18
bezendu:
Nie da się bez podobieństwa..? Jestem w tym słaby a co dopiero w bryłach to zauważyć.
12 lut 16:26
Bizon:
... przecież, to trójkąty na jednej ścianie bocznej ... oba prostokątne i w obu jednym z kątów
jest ∡BCG ...
12 lut 17:40
Mila:
Do rys. 12:18
1) Oblicz BG, potem DF w zależności od k i a, |DF|=
√k2−(1/4)a2
| | 1 | |
PΔBCD= |
| *a*|DF| porównaj pola |
| | 2 | |
oblicz k
2
3) Oblicz H
12 lut 17:57
bezendu:
Tylko, że ja nie rozumiem nic z tych zależności.
12 lut 17:59
Mila:
Co umiesz obliczyć?
12 lut 18:05
bezendu: Przy tych danych nic.
12 lut 18:06
Mila:
Do rys. 12:18
ΔABG− Δrównoramienny
ΔGEB− Δprostokatny
EB=sinα*BG
BG jest wysokością ΔBCD,
WΔDFC: DC=k
|DF|=
√k2−0,25a2
| | 1 | | 1 | |
PΔBCD= |
| *a*|DF|= |
| *a*√k2−0,25a2 |
| | 2 | | 2 | |
| 1 | | 1 | | a | |
| *a*√k2−0,25a2= |
| *k* |
| oblicz k2, a potem z tw. Pitagorasa H |
| 2 | | 2 | | 2sinα | |
Dalej sam
12 lut 18:25
bezendu:
Dziękuję bardzo. Ale te zadania z literkami chyba nie są dla mnie.
12 lut 18:28
Mila:
Nie panikuj. Postaraj się zaraz dokończyć, bo później wyrzucę kartkę z obliczeniami.
Przecież umiesz przekształcac wzory.
Analizuj i ucz sie. Na studiach nikt nie będzie Cię tego uczył.
12 lut 18:36
bezendu:
Jak mam nie panikować jak już niedługo matura, a nie potrafię tego ?
12 lut 18:37
Mila:
Analizuj, zapisuj na kartce, postaraj się zrozumieć, na pewno potrafisz!
12 lut 18:40
bezendu:
Już trzeci raz zabieram się za to zadanie i niestety nic. Nie dam rady dokończyć.
12 lut 18:44
Mila:
No to dalej tak:
Spróbujesz dalej?
12 lut 19:00
bezendu:
Proszę o rozwiązanie do końca..
12 lut 19:01
Mila:
cd.
| | 4sin2α−1 | | a2 | |
k2*( |
| )= |
| |
| | 4sin2α | | 4 | |
| | a2 | | 4sin2α | |
k2= |
| * |
| |
| | 4 | | 4sin2α−1 | |
Teraz obliczymy H:
| | 2 | | 2 | | a√3 | |
W ΔDOC: |OC|= |
| h= |
| * |
| |
| | 3 | | 3 | | 2 | |
| a2*sin2α | | a2 | |
| − |
| =H2 sprowadzam do wspólnego mianownika |
| 4sin2α−1 | | 3 | |
| | 3sin2α−(4sin2α−1) | |
H2=a2 |
| |
| | 3*(4sin2α−1) | |
| | 1−sin2α | | cos2α | |
H2=a2* |
| =a2* |
| |
| | 3*(4sin2α−1) | | 3*(4sin2α−1) | |
Oblicz V
12 lut 19:20
bezendu:
| | 1 | | a2√3 | | acosα | |
V= |
| * |
| * |
| |
| | 3 | | 4 | | √3(4sin2α−1) | |
| | a3√3cosα | |
V= |
| j3 |
| | 12√3(4sin2α−1) | |
12 lut 19:25
Mila:
Możesz jeszcze uprościć przez √3.
Postaraj się zrozumeć to porównywanie pola Δ, albo zacznij rozpoznawac Δ podobne.
Może jutro z podobieństwa rozwiążemy?
12 lut 19:43
bezendu:
Może być, choć ja jestem słaby z planimetrii i mam problem z podobieństwem więc wątpię czy dam
radę. A za rozwiązanie dziękuję bo wymagało dużo pisania.
12 lut 19:44
Mila:
Teraz jeszcze raz wszystko sam rozwiąż, najpierw plan, potem po kolei obliczenia.
12 lut 19:45
bezendu:
Ja bym BG policzył wgl z twierdzenia cosinusów
12 lut 19:48
Mila:
Też tak liczyłam, ale myślałam, że korzystasz ze wskazówki [b{Bizona]]. To jest prościej.
12 lut 19:52
bezendu:
Za dużo zależności. Wrócę jutro do tego zadania, może zrozumiem a teraz idę robić inne bryły.
12 lut 19:55