Sterometria Ostrosłup
Damian: Podstawą ostrosłupa jest romb, którego bok ma długość 13 cm, a długość jednej przekątnej jest
równa 24 cm. Długość drugiej przekątnej jest równa długości wysokości ostrosłupa. Oblicz
objętość ostrosłupa
30 mar 11:54
Damian: chyba nikt nie potrafi tego zrobic ...
30 mar 12:24
Hajtowy: Ty potrafisz, ale chyba o tym nie wiesz

30 mar 12:25
Hajtowy:
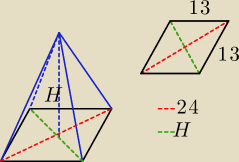
30 mar 12:29
Damian: nie potrafie jedynie obliczyć wysokości w tym rombie .
h=?
a=13 cm
d2=24cm
d1=H
d1= 10 cm= H
V= 1/3*Pp*H (pole rombu a*h = a2 * sinα )
a czy moge skorzystać z wzoru na pole rombu " 1/2 d1 *d2"
30 mar 12:33
30 mar 12:35
Damian: faktycznie nie doczytałem na wzorach tej zalezności pola
e*f2
zadanie zrobione dzieki za pomoc

30 mar 12:38
pigor: ... z warunków zadania i własności rombu połowa
krótszej przekątnej jest równa z tw. Pitagorasa :
e
2=13
2−12
2=1*25 ⇒ e=5 i
H=2e=
10 − wysokość ostrosłupa,
więc pole podstawy (rombu)
Pp=12*24*10=12*10=
120, zatem
Vo=13P
p*H=
13*120*10=40*10=
400 [cm3] − szukana objętość.

30 mar 12:39


 https://matematykaszkolna.pl/strona/866.html
https://matematykaszkolna.pl/strona/866.html


