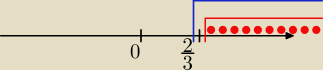dziedzina olka13: oblicz dziedzinę funkcji f(x) = 1 / (√3x−2)

5-latek: dziedziny sie nie oblicza . dziedzine sie wyznacza(okresla . Mianownik ≠0 i to co pod pierwiastkiem ≥0

Olgaaa: 3x−2>0 i dalej jedziesz

5-latek: Ale w zwiazku z tym z e mianownik nie moze rownac sie 0 wiec to co jest pod pierwiaskiem ma byc >0

5-latek: OLga spojrz tu https://matematykaszkolna.pl/forum/244237.html

olka13: a mam takie pytanie czy jest jakaś różnica w wyznaczaniu dziedziny pomiędzy : a) y = √2x²−2x−3 b) y = 1 / (√2x²−2x−3) w obu przypadkach przyrównuje 2x²−2x−3 ≥ 0 czy w którymś tylko "> 0 "

5-latek: napisalem CI to dokladnie W drugim to co pod pierwiastkiem musi byc >0 (nie moze byc ≥0 bo przez 0 dzielic nie wolno W pierszej funkcji ma byc >=0

Dziadek Mróz:

	a
f(x) =
	b

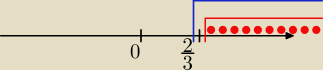
D: b > 0 b = √c D: c ≥ 0

	1
f(x) =
	√3x−2

D: √3x − 2 > 0 ⋀ 3x − 2 ≥ 0 3x − 2 > 0 ⋀ 3x − 2 ≥ 0 3x − 2 > 0 3x > 2 x > ²₃ 3x − 2 ≥ 0 3x ≥ 2 x ≥ ²₃ D: x > ²₃ ⋀ x ≥ ²₃ => x > ²₃ ∩ x ≥ ²₃ => x > ²₃