.
Ksia: Wie ktoś bo ja nie mam pojęcia jak się za to zabrać ? W kuli o promieniu R umieszczono 4
przystające kulki. Jaką największą wartość może przyjąć suma ich objętości.
27 mar 18:29
Mila:
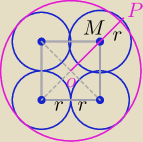
|OP|=R
|OM|=połowa przekątnej kwadratu o boku 2r
Ułóż równanie i oblicz r.
Potem oblicz V
Poradzisz sobie?
27 mar 18:48
Ksia: chyba nie , nie wiem się jak za to zabrać
28 mar 10:45
J:
Masz kwadrat o boku 2r , zatem jego przekątna d = 2r√2 i jej połowa x = r√2
Teraz x + r = R i obliczasz r , a potem objętość 4 kulek
28 mar 10:52
Ksia: a jak się za to zabrać bo za nic nie mogę tego ogarnąć ?
28 mar 10:53
J: Kasiu .. , a do jakiej Ty chodzisz szkoły ?
28 mar 10:55
Ksia: po prostu nie jestem z tego dobra , a stereometrie dopiero zaczełam się uczyć a nauczyciele
takie zadanka dają bez wyjasnienia i jak żyć
28 mar 10:57
5-latek: J . Podejrzewam ze do liceum (stereometria − to ktora klasa ?
Nie zdziwilbym sie zeby to byla mayturzystka
28 mar 10:58
J:
Tu masz przekrój, wiec to już planimetria. Masz już wskazówki, wiec to już algebra.
r√2 + r = R , spróbuj obliczyć r z tego równania.
28 mar 10:59
Ksia: jakie to ma znaczenie , po co drązyć temat , to jak pomożesz , proszę
28 mar 11:00
5-latek: Jak zyc to oto musisz zapytac naszego premiera
x+r=r za x podstaw r
√2
r
√2+r=R
r(
√2+1)=R
r= mozesz usunac niewymiernosc z mainownika i dzialaj dalej sama
28 mar 11:02
5-latek: Oczywiscie ma byc x+r=R
28 mar 11:05
J: I tak już podałeś r =

28 mar 11:05
5-latek: J
Powiem CI ze to jest i smieszno i straszno skoro nie umie rozwiazywac takich rownan.
Mam tylko taka nadzieje ze wzor na objetosc kuli zna
28 mar 11:11
Ksia: może i śmieszno,strasznie ale co poradzisz , ale już nadrabiam zaległośc a i wzór zna zna
28 mar 11:12
J: No to po zadaniu. Oblicz objętość jednej kulki i wynik pomnóż prze 4.
28 mar 11:14
Ksia: ok

poradzę sobie już i serdecznie dziękuję

, wiem że macie świetny ubaw , ale takie życie
nie każdy jest ze wszystkiego orłem , mam jeszcze 1 zad ale sama spróbuje zrobić
28 mar 11:16
5-latek: Kasiu w zadnym wypadku to nie jest ubaw .
W takim rownaniu musisz skorzystac z tej wlasnosci dzialan na liczbach rzeczywistych
(wyciaganie wspolnego czynnika przed nawias
Otoz jesli mamy a*c+b*c=c(a+b)
UNas a=√2 i b=1 a c=r wyciagasz r przed nawias i masz r(√2+1) bo eraz w druga strone
r*√2+r*1= r√2+r
czy naprawde nikt wam tego nie tlumaczy ?
Pewnie ze nikt nie jest orlem (to samo mowie w pracy ale skoro robie wiecej i umie wiecej to
chcialbym wiecej zarabiac Nie ?
28 mar 11:25
5-latek: No a co to za zadanie ktore masz jeszce do zrobienia ?
28 mar 11:32
Ksia: no niestety nie olewka kompletna , zgadzam się z tym co mówisz , ale żeby płacili adekwatnie od
tego to byłbyś milionerem pewnie ,

ale dobra to już wiem jak skończyć , ale w miedzy czasie
robiłam takie zadanko cytuję ,,wyznacz kąt dwuścienny między ścianami bocznymi w ostrosłupie
prawidłowym czworokątnym '' i narysowałam , wyznaczyłam i czy trzeba do tego jakies obliczenia
robic , bo w zadaniu nie pisze nic o obliczeniach ?
28 mar 11:36
PW: A teraz doleję łyżkę dziegciu.
Kto wytłumaczy, dlaczego taka czwórka kulek spełnia warunki zadania (daje maksymalną objętość).
Według mnie to jest najważniejsza kwestia w tym zadaniu, a szanowni przedmówcy przyjmują
milcząco, że skoro ktoś coś narysował, to to coś jest dobre.
Pytam zupełnie poważnie. Mam słabą wyobraźnię przestrzenną i rysowanie idzie mi mozolnie, ale
to jest sprawa drugorzędna − żaden rysunek nie jest dowodem, że to co narysowaliśmy jest
"maksymalne". Jak wiadomo intuicja bywa zawodna.
28 mar 11:39
5-latek: Skoro nie masz danych to nie potrzeba obliczen
28 mar 11:39
Ksia: o to dzięki za odpowiedź

bo podobnie też tak myślałam , a o co chodzi PW ?
28 mar 11:41
J: https://matematykaszkolna.pl/forum/243915.html . Wdaje mi się,ze jednak ten wariant nie jest do końca prawidłowy. Mówimy o kulach
przystających ( co to znaczy), a tutaj, w tym podejściu do rozwiązania kule są raczej "parami
przystające.Bardziej przemawia do mne ta wersja, kule maja ten sam promień.
28 mar 11:58
Ksia: kurcze no tylko nie mów że to to jest źle

28 mar 12:06
J: Nie ... ja tylko mówię,że właśnie kulki mają mieć ten sam promień, tak jak tutaj w tym
rozwiązaniu.
28 mar 12:11
Ksia: a wykonałbyś obliczenia , bo tam jakoś dziwnie jest napisane , to będę miała 2 wersję , bo ten
sysunek daje do myslenia , mógłbyś ?
28 mar 12:17
pigor: ..., ja bym bardzo i na serio pomyślał tu i teraz o...

przypadku 3−ech kulek stycznych między sobą i tej 4−tej na
nich w środku, czyli w "dołku" utworzoym przez te 3−y ...

28 mar 12:36
Ksia: Ciekawa teoria czyli myślisz że w tej kuli znajduje się ta jedna kulka , a na niej leżą
rozłożone 3 kulki , ale ja wiem , mi się zdaje że chodzi o to że w tej jednej kuli , są takie
same kulki , i pod tym kątem rozwijam tok myslenia
28 mar 12:44
pigor: ... , chyba się nie rozumiemy; w danej jednej duuużej kuli
w płaszczyźnie jej średnicy leżą styczne do siebie i każda do tej dużej
takie same 3 małe kulki i pod
albo nad nimi (te trzy utworzą
w środku bardzo mały, ale istotny "dołek") leży 4−ta identyczna mała
kulka..
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
wyobraź sobie to, patrząc na to co powiedziałem jak na przekrój środkowy dużej kuli
z góry, ale wtedy "widzisz" 3 kulki wewnątrz dużego koła ( nie jak u
Mili 4 male kulki)
i tę 4−tą na nich (albo pod nimi) w środku dużej kuli . ..

−−−−−−−−−−−−−−−−−−−−−−−
..

mam nadzieję, że
Mila ci to pięknie narysuje

., bo ja nie mam i nie chcę mieć
(przepraszam) pojęcia jak się rysuje w tym edytorze .
28 mar 13:12
Ksia: rozumiem o czym mówisz , może wczesniej źle to sformuowałam , wporządku rozumiem , ale dzięki
że dałeś mi dużo do zrozumienia , a jak trafić do Mili ?
28 mar 13:17
pigor: ... , powtarzam, oczywiście wszystkie "moje" małe 4 kulki o których
...

opowiedziałem są do siebie przystające (takie same), styczne z sobą
i z 5−tą zewnętrzną dużżą kulą . ufff . ...

28 mar 13:17
Ksia: już wiem sorki głupie pytanie

28 mar 13:18
pigor: ..., jak trafić

nie trafić tylko, ładnie ją tu poprosić

,a
na pewno usłyszy i jak tylko będzie miała czas spełni twoją prośbę

28 mar 13:21
Ksia: ok , to ją bardzo ładnie poproszę

tylko nie wiem czy w tym poście do niej pisać czy jak bo
jestem tu szczerze mówiąc nowa i nieoblatana w temacie
28 mar 13:24
pigor: ... , a tak jeszcze dopowiem i ...

znikam już naprawdę, coś mi wygląda,
że wtedy środki tych 4−ech małych kulek utworzą piękny czworościan foremny
o krawędzi długości 2r − średnicy tych kuleczek . ..

28 mar 13:26
pigor: ..., tak w tym poście

28 mar 13:27
Ksia: Droga Mila ,bardzo ale to bardzo proszę o pomoc w tym zadaniu bo każdy ma inny tok
myslenia a ja chcę je mieć dobrze zrobione i wyjasnione co i jak bo chciałabym to zrozumieć ,
a zaczynam mieć mętlik . Pomożesz jeśli będziesz w stanie i oczywiście jeśli będziesz miała
czas ?
28 mar 13:52
Mila:
Myślę nad rysunkiem przestrzennym. ( Cztery kłębki włóczki ( kule) mam przed sobą)
Rysunek z 18:48 pasuje do kul wpisanych odpowiednio w walec. Szkoda,że dopiero dzisiaj się
odezwałaś.
Kule o jednakowych promieniach r są ułożone w kuli o promieniu R, tak , aby były największe,
to muszą być tak "utkane", że ich środki są wierzchołkami czworościanu foremnego o krawędzi
2r.
(to pisze właśnie kolega
Pigor)
Promień kuli opisanej na czworościanie foremnym o krawędzi 2r wynosi: ( patrz wzory, albo
| | 3 | |
wyprowadź, jako R= |
| H, H − wysokość czworościanu foremnego) |
| | 4 | |
Promień kuli opisanej na tych czterech małych kulach jest większy o r.
2R=2r+r
√6
2R=r(2+
√6) /(
√6−2})
2R(
√6−2)=r*(6−4)
2R*(
√6−2)=2r
r=R*(
√6−2)
Rysunek później.
(
Pigor , PW, ? zgadzacie się teraz z modelem?
28 mar 19:12
Ksia: wybacz że później nie zerknęłam bo arkusze rozwiązywałam Ok dziękuję

bo już miałam mętlik i
nie wiedziałam co idzie w dobrym kierunku

28 mar 19:17
Ksia: Dobrze
28 mar 19:18
Mila:
Nie wiem, co oznacza Twoje dobrze, czy wynik zgodny z odpowiedzią, czy ...?
28 mar 19:22
Mila:
Będę za pół godziny.
28 mar 19:22
Ksia: wynik miałam inny , poprostu spaprałam , dobrze oznaczało że poczekam na twój rysunek ,
28 mar 19:27
Mila:
Jednak ten układ pierwszy też możemy rozważać.
Kolega obliczył promień małej kuli ( oznaczę r
1), możesz porównać te dwa promienie.
r
1=R*(
√2−1)
Różnica niewielka, ale
√6−2>
√2−1
28 mar 19:59
Ksia: ok nadążam
28 mar 20:09
Ksia: no dobra mam to, to teraz wystarczy obliczyć objętość 1 kuli razy 4 (chodzi mi o te kulki
znajdujace sie w srodku ?
28 mar 20:21
28 mar 20:22
Mila:
Tak ,obliczasz objętość jednej kulki i mnożysz przez 4.
(√6−2)3 =(√6−2)2*(√6−2) tak licz sześcian tego wyrażenia.
Masz odpowiedzi do zadania?
28 mar 20:25
Ksia: ok spróbuje to sobie zbudować , ok to zaraz obliczę objętość , a odpowiedzi nie mam bo to mam
zaprezentować na egz. ustnym semestralnym JUTRO i chcę się jak najlepiej przygotować
28 mar 20:31
Mila:
W jakiej szkole?
28 mar 20:33
Ksia: zaocznie weekendowo

gdybym miała stacjonarnie , pewnie bym takich problemów nie miała
28 mar 20:35
Mila:
To podaj dwa przypadki rozłożenia kul, jak na zaoczne, to za trudne te zadania.
28 mar 20:37
Ksia: no trudne ale jak matura za miesiąc to musi być ciężko

ale trzeba próbować , z tymi
przypadkami chodzi o to kiedy ta wartość jest największa wtedy, gdy kule są styczne do siebie
i
do kuli dużej , o to ci chodzi ?
28 mar 20:40
Mila:
1) są styczne jak pokazałam na pierwszym rysunku (wtedy mniejsz wychodzi promień)
2) są styczne jak masz na drugim rysunku ( wtedy wychodzi promień większy i objętość będzie
większa.
28 mar 20:56
Ksia: aha , to mam prośbę pomożesz mi to wszystko upleść te wszystkie działania chronologicznie
(rysunki nie ) bo mi się teraz to wszystko pomieszało , i czuję że robi mi się masło maślane ?
28 mar 21:02
Bogdan:
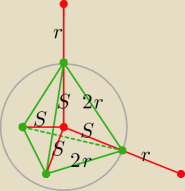
Szkic do tego zadania mógłby być taki.
Środki czterech stycznych do siebie kul o promieniu r są wierzchołkami czworościanu
foremnego, każda krawędź tego czworościanu ma długość 2r.
| | r√6 | |
S − długość promienia kuli opisanej na czworościanie foremnym o krawędzi 2r, S = |
| |
| | 2 | |
| | r√6 | |
R = S + r ⇒ R = |
| + r ⇒ r = R(√6 − 2) |
| | 2 | |
28 mar 21:34
Mila:
Piękny rysunek
Bogdanie.

.
28 mar 21:45
Mila:
Kasiu,
Napisz obliczenia z 19:12 i rysunek Bogdana.
28 mar 21:48
Ksia: No pięknie

 Bogdanie
Bogdanie
28 mar 21:50
PW: Teraz jestem przekonany. Proszę − jak łatwo czasem coś uzasadnić "od tyłu" − nie wpisywać kulek
do dużej kuli, tylko na czterech ciasno ułożonych kulkach opisać dużą.
28 mar 21:54
Ksia: oki , mam to już , a te obilczenia z 19:59 tez uwzględnić?
28 mar 21:55
Mila:
Możesz uwzględnić, ale pierwszy rysunek dołącz.
28 mar 22:01
Ksia: rysunek już jest , obliczenia też , a jak teraz z objętością ?
28 mar 22:03
PW: Tak, jest to bardzo ważne. "Ciasno ułożone 4 kulki" mogą leżeć płasko na stole, a mogą tworzyć
"piramidkę" jak to narysował Bogdan. To jest najważniejsze w zadaniu − rozstrzygnąć,
które ułożenie pozwala opisać większą kulę (czy odwrotnie − przy którym ułożeniu promienie
małych kulek będą większe).
28 mar 22:05
Mila:
V obliczasz z wzoru na objętość, większy promień to większa objętość, dla mniejszego nie musisz
już liczyc.
28 mar 22:29
Bogdan:

28 mar 22:33
Ksia: ok już wszystko obliczyłam , i ja już zmykam ,dziękuję wam wszystkim za pomoc

, Odezwę się
jutro wieczorem w tym poście i dam znać co powiedziała nauczycielka .
28 mar 22:39
Ksia: Dzięki wielkie za pomoc
Mila ,
Bogdan,
PW,
Pigor,
5−latek udało się co
prawda były lekkie zastrzeżenia bo stwierdziła że chodziło jej o coś innego ale podobała się
ta wersja, Jeszcze raz wielkie dzięki

29 mar 20:38
Mila:
A wyjaśniła Ci o co chodziło? Treść zadania powinna byc podana jednoznacznie.

29 mar 22:13
Ksia: Nie, zbyła mnie , no sama chciałam się dowiedzieć ale nie wyszło , ale naprawdę szczere dzięki
za pomoc , jeśli jeszcze będe miała jakieś problemy z matmą to mogę się do cb zgłosić , jeśli
oczywiście zechcesz

29 mar 22:50
Mila:
Tak

29 mar 22:57
 |OP|=R
|OM|=połowa przekątnej kwadratu o boku 2r
Ułóż równanie i oblicz r.
Potem oblicz V
Poradzisz sobie?
|OP|=R
|OM|=połowa przekątnej kwadratu o boku 2r
Ułóż równanie i oblicz r.
Potem oblicz V
Poradzisz sobie?

 Powiem CI ze to jest i smieszno i straszno skoro nie umie rozwiazywac takich rownan.
Mam tylko taka nadzieje ze wzor na objetosc kuli zna
Powiem CI ze to jest i smieszno i straszno skoro nie umie rozwiazywac takich rownan.
Mam tylko taka nadzieje ze wzor na objetosc kuli zna
 poradzę sobie już i serdecznie dziękuję
poradzę sobie już i serdecznie dziękuję  , wiem że macie świetny ubaw , ale takie życie
nie każdy jest ze wszystkiego orłem , mam jeszcze 1 zad ale sama spróbuje zrobić
, wiem że macie świetny ubaw , ale takie życie
nie każdy jest ze wszystkiego orłem , mam jeszcze 1 zad ale sama spróbuje zrobić
 ale dobra to już wiem jak skończyć , ale w miedzy czasie
robiłam takie zadanko cytuję ,,wyznacz kąt dwuścienny między ścianami bocznymi w ostrosłupie
prawidłowym czworokątnym '' i narysowałam , wyznaczyłam i czy trzeba do tego jakies obliczenia
robic , bo w zadaniu nie pisze nic o obliczeniach ?
ale dobra to już wiem jak skończyć , ale w miedzy czasie
robiłam takie zadanko cytuję ,,wyznacz kąt dwuścienny między ścianami bocznymi w ostrosłupie
prawidłowym czworokątnym '' i narysowałam , wyznaczyłam i czy trzeba do tego jakies obliczenia
robic , bo w zadaniu nie pisze nic o obliczeniach ?
 bo podobnie też tak myślałam , a o co chodzi PW ?
bo podobnie też tak myślałam , a o co chodzi PW ?

 przypadku 3−ech kulek stycznych między sobą i tej 4−tej na
nich w środku, czyli w "dołku" utworzoym przez te 3−y ...
przypadku 3−ech kulek stycznych między sobą i tej 4−tej na
nich w środku, czyli w "dołku" utworzoym przez te 3−y ... 
 −−−−−−−−−−−−−−−−−−−−−−−
..
−−−−−−−−−−−−−−−−−−−−−−−
.. mam nadzieję, że Mila ci to pięknie narysuje
mam nadzieję, że Mila ci to pięknie narysuje  ., bo ja nie mam i nie chcę mieć
(przepraszam) pojęcia jak się rysuje w tym edytorze .
., bo ja nie mam i nie chcę mieć
(przepraszam) pojęcia jak się rysuje w tym edytorze .
 opowiedziałem są do siebie przystające (takie same), styczne z sobą
i z 5−tą zewnętrzną dużżą kulą . ufff . ...
opowiedziałem są do siebie przystające (takie same), styczne z sobą
i z 5−tą zewnętrzną dużżą kulą . ufff . ... 

 nie trafić tylko, ładnie ją tu poprosić
nie trafić tylko, ładnie ją tu poprosić  ,a
na pewno usłyszy i jak tylko będzie miała czas spełni twoją prośbę
,a
na pewno usłyszy i jak tylko będzie miała czas spełni twoją prośbę 
 tylko nie wiem czy w tym poście do niej pisać czy jak bo
jestem tu szczerze mówiąc nowa i nieoblatana w temacie
tylko nie wiem czy w tym poście do niej pisać czy jak bo
jestem tu szczerze mówiąc nowa i nieoblatana w temacie
 znikam już naprawdę, coś mi wygląda,
że wtedy środki tych 4−ech małych kulek utworzą piękny czworościan foremny
o krawędzi długości 2r − średnicy tych kuleczek . ..
znikam już naprawdę, coś mi wygląda,
że wtedy środki tych 4−ech małych kulek utworzą piękny czworościan foremny
o krawędzi długości 2r − średnicy tych kuleczek . ..

 bo już miałam mętlik i
nie wiedziałam co idzie w dobrym kierunku
bo już miałam mętlik i
nie wiedziałam co idzie w dobrym kierunku
 gdybym miała stacjonarnie , pewnie bym takich problemów nie miała
gdybym miała stacjonarnie , pewnie bym takich problemów nie miała
 ale trzeba próbować , z tymi
przypadkami chodzi o to kiedy ta wartość jest największa wtedy, gdy kule są styczne do siebie
i
do kuli dużej , o to ci chodzi ?
ale trzeba próbować , z tymi
przypadkami chodzi o to kiedy ta wartość jest największa wtedy, gdy kule są styczne do siebie
i
do kuli dużej , o to ci chodzi ?
 Szkic do tego zadania mógłby być taki.
Środki czterech stycznych do siebie kul o promieniu r są wierzchołkami czworościanu
foremnego, każda krawędź tego czworościanu ma długość 2r.
Szkic do tego zadania mógłby być taki.
Środki czterech stycznych do siebie kul o promieniu r są wierzchołkami czworościanu
foremnego, każda krawędź tego czworościanu ma długość 2r.
 .
.

 Bogdanie
Bogdanie

 , Odezwę się
jutro wieczorem w tym poście i dam znać co powiedziała nauczycielka .
, Odezwę się
jutro wieczorem w tym poście i dam znać co powiedziała nauczycielka .



