, Radek: Rafał28 jesteś ?

Rafał28: jestem

Radek: To dziś też działamy ?

Rafał28: można, mam 2h

Radek: 1. Dane są punkty A = (− 4,32) i B = (−3 6,16) . Wykaż, że koło o średnicy AB jest zawarte w II ćwiar tce prostokątnego układu współrzędnych Wystarczy policzyć środek odcinak tylko ?

Rafał28: Środek odcinka tak. Później musisz ocenić czy to koło się zmieści w II ćwiartce. Czyli jak to zrobisz?

Radek: Policzyć promień.

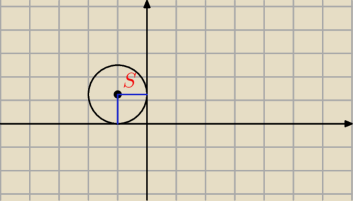
Rafał28: Promień też się przyda.

Radek: I jeszcze coś trzeba ? czy to wystarczy ?

Rafał28: Punkt S ma współrzędne S(x, y). Takie wyliczyłeś. Odległość punktu S od osi OY oraz odleglość punktu S od osi OX musi być równa promieniowi

Rafał28: znaczy nie równa, większa lub równa promieniowi

Radek: i pokazać, że środek jest oddalony o mniej niż odległość punktu od osi OY tak ? promień<odległość od osi OY ?

Rafał28: tak. promień ma być mniejszy od odległości środka S okręgu od osi OY, czyli od odcinka prostopadłego do osi OY

Rafał28: Takie warunki wystarczą bo punkty A, B są w II ćwiartce, czyli środek AB też jest w drugiej ćwiartce.

Radek: 2.Wyznacz współrzędne środka ciężkości trójkąta w zależności od współrzędnych jego wierzchołków

Rafał28: Środkowe przecinają się w jednym punkcie w stosunku 2:1 licząc od wierzchołka trójkąta.

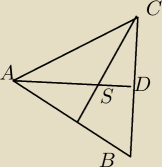
Rafał28: Oznacz wierzchołki A(x_a, y_a); B(x_b, y_b); C(x_c, y_c) Jakiś pomysł?

Radek: Napisać równania środkowych ?

Rafał28: D jest środkiem BC. Wyznacz jego współrzędne. Później skoro środkowe przecinają się w stosunku 1:2 to znaczy, że |AS| = 2x oraz |DS| = x (x jest dla przykładu) |AD| = 3x

	|AS|		2x
Wobec tego		=		= 23
	|AD|		3x

czyli AS^→ = ²₃AD^→ a tam już uzyskamy współrzędne środka S, wystarczy przyrównać i policzyć

Radek: A mogę wiedzieć czemu AD=3x ?

Rafał28: bo skoro przyjęliśmy sobie, że |AS| = 2x oraz |SD| = x to suma tych odcinków daje nam 3x. dla x>0 x jest tylko przykładowe, może to być dowolna literka. Ważne, że te odcinki dzielą się w stosunku 1 : 2

Radek: Trzeba to robić wektorami ?

Rafał28: To geometria analityczna. Inaczej się nie da. Punktu A(x_a, y_a); B(x_b; y_b) Wyznaczamy wektor według wzoru: AB^→ = [x_b − x_a, y_b − y_a]

Radek: Próbuje zawsze obejść sposób wektorowy.

Rafał28: AS^→ = ²₃AD^→ Najpierw punkt D jako środek dwóch innych punktów a później działania na wektorach.

Radek: Znajdź równanie prostej k przechodzącej przez punkt P(2 ,5) , która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36

Rafał28: czekaj jeszcze raz obliczenia bo mi wyszło dziwne równanie

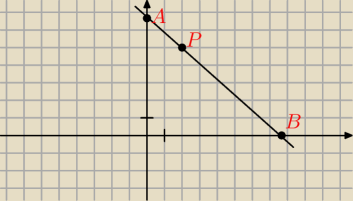
Rafał28: Prosta ma równanie y = ax + b Punkt P(2, 5) należy do tej prostej, czyli 5 = 2a + b Z tego wyznaczamy b b = 5 − 2a Wobec tego nasza prosta przyjmuje postać y = ax + 5 − 2a

Rafał28: Teraz pozostaje wyznaczyć współrzędne punktów A, B wiedząc, że punkt A leży na osi OY czyli pierwsza współrzędna to x_a = 0 oraz punkt B lezy na OX, czyli y_b = 0 oraz wiedząc, że punktu A, B należą do prostej y = ax + 5 − 2a

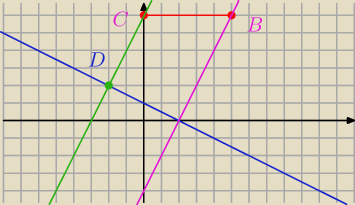
Radek: Punkty B = (5,6) i C = (0,6) są wierzchołkami trapezu równoramiennego ABCD , którego podstawy

	1
AB i CD są prostopadłe do prostej k o równaniu y = −		x + 1 . Oblicz współrzędne
	2

pozostałych wierzchołków trapezu, wiedząc, że punkt D należy do prostej k . Jak wyznaczyć punkt A ?

Rafał28: Tamte zadania zrobiłeś? Co do obecnego zadania Wyznacz prostą prostopadłą do prostej k i przechodzącą przez punkt B. Nazwijmy ją prostą m. Punkt wspólny prostej k i prostej m to punkt A.

Radek: Tak zrobiłem, a chcę zrobić jak najwięcej jak jesteś na forum. A=(0,2) ?

Rafał28: A =(2, 0) na rysunku nawet widać

Rafał28: Patrz jak masz prostą prostpadłą w postaci ogólnej 5x + 87y − 325 = 0 To prosta prostopadła do niej wynosi −87x + 5y + C = 0 (C dowolne) Czyli zamieniłem tylko dwie wartości Ax + By + C = 0 oraz prostopadła do niej −Bx + Ay + D = 0

Radek: Ale w odp mam dwa wyniki co do A.

Rafał28: nie przeczytałem, że to trapez równoramienny

Radek: (2,0) to też zła odp

Rafał28: Ale dobrze było. Należy wyznaczyć prostą prostopadłą do k i przechodzącą przez punkt C. Wtedy punkt wspólny tych prostych to punkt D. Następnie wyznaczyć prostą prostopadłą do prostej k i przechodzącą przez punkt B. Już to policzyliśmy ta prosta wynosi. y=2x−4 Punkt A należy do tej prostej, czyli ma współrzędne A=(x, 2x−4) Ostatnie co należy zrobić to |AD| = |BC| z wektorów

Radek: Ja zrobię to z długości odcinka.

Rafał28: ok

Radek: Dany jest okrąg o równaniu x² y²−2x+6y+5= 0 . Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu x − 2y = 0 . Wiem jak napisać styczne do okręgu jak mają przechodzić przez jakiś punkt ale tutaj mam problem (x−1)²+(y+3)²=5 x−2y=0 −2y=−x

	1
y=		x+b
	2

Rafał28: x−2y=0 2y = x y = ¹₂x

Radek: a nie +b jeszcze ?

Radek: −2x+b o tak jak już

Rafał28: tak, tak

⎧	y = 12x + b
⎨
⎩	równanie okręgu

Rafał28: czekaj, czekaj tak napisałem co mi nos podpowiada, policzę też coś

Radek: Ok, to sobie dokończę a teraz następne: Mam A=(5,7) B=(−9,−7) C=(−1,9) jak napisać rówanie okręgu opisnago na tym trójkącie ?

Rafał28: Już widzę Trzeba wyznaczyć prostą prostopadłą do prostej y = ¹₂x oraz przechodzącą przez środek okręgu. Później prostą prostopadłą do ostatniej przechodzącą przez środek okręgu. Prosta ta przetnie środek okręgu w dwóch punktach. Aby wyznaczyć te punkty to trzeba rozwiązać układ równań z

⎧	równanie okręgu
⎨
⎩	ostatnia prosta

jak masz punkty to prowadzisz styczne prostopadłe do prostej y= ¹₂x przechodzące przez te punkty.

Rafał28: Okrąg opisany na trójkącie ma środek w punkcie przecięcia się środkowych (środek cieżkości). Tak się składa, że już poznałeś wzór na wyznaczenie tego środka wcześniej mając 3 wierzchołki trójkąta . Później promień okręgu to dowolna odległość |AS| = |BS| = |CS| = R

5-latek: https://matematykaszkolna.pl/strona/541.html zobacz gdzie lezy srodek okregu opisanego na trojkacie (wiec wyznacz go i np odleglosc punkrtu A o srodka to promirn okregu To jest 1 sposob

Piotr 10: Rafał chyba jednak pomyliłeś się

Radek: albo można z układu równań. Pani Mila kiedyś pokazywała. Dobra DZIĘKUJĘ Ci Rafał za pomoc

Piotr 10: Tak możesz układ 3 równań

Radek: a w przypadku wpisanego ?

Rafał28: tak tak oczywiście o symetralne chodzi

Piotr 10: W przypadku wpisanego, nie można już tak samo jak( uklad 3 rownan). Proponowałbym, tak policzyć pole tego trójkąta, następnie długości boków a potem ze wzoru P=r*p , gdzie r− promień okregu wpisanego w trojkąt

Rafał28: Ogólnie lepiej z wyznaczników to liczyć

Radek: z metody wyznaczników ?

5-latek: Albo jesli znasz wzory na cosinusy kierunkowe wektora wynaczysz rownania dwusiecznych (wystarczy 2 i punkt przciecia tych dwusiecznych to srodek okregu wpisananego w trojkat

Rafał28: P_ABC = ¹₂|det(AB^→, AC^→)| nie wym czy wyznaczniki są w szkole? chyba są mamy dwa wektory AB^→ = [a₁, a₂] AC^→ = [b₁, b₂] Wtedy det(AB^→, AC^→) = a₁b₂ − a₂b₁ i zero symetralnych, środków boków i dalszego cudowania

Radek: znam metodę wyznaczników ale nie wiem jak liczyć tym, może jutro bardziej szczegółowo.

Rafał28: uciekam Dobranoc.

zawodus: W karcie wzorów jest bez wyznaczników

5-latek: czesc zawodus Ale wkarcie wzorow tez pewnie nie ma cosinusow kierunkowych wektora z ktorych mozesz wyznaczych kierunek dwusiecznej kata

Radek: ?

Radek: ?