dowód Saizou : dowodzik dla chętnych wykazać że jeśli a²+b²≤2 to a+b≤2

Eta:

Saizou : taki z dzisiejszej lekcji

razor: nierownosc miedzy srednia kwadratowa i arytmetyczna? dobrze mysle?

Saizou : jestem ciekaw jak to zrobisz

anita22: to trzeba takie coś udowadniać

Saizou : poczekam na pełne rozwiązanie

razor:

	a2 + b2		a2 + b2
a2 + b2 ≤ 2 ⇒		≤ 1 ⇒ √		≤ 1
	2		2

	a2 + b2		a+b
ze srednich √		≥		zatem
	2		2

	a2 + b2		a+b
2 ≥ 2√		≥ 2		= a+b
	2		2

2 ≥ a + b

Godzio: Też jestem za propozycją razora

Eta:

Saizou :

Godzio: Saizou masz coś trudnego ? (mogę się odwdzięczyć tym samym )

Maslanek: Rzuć coś ciekawego Chętnie popatrzę

Maslanek: Rzuć coś ciekawego Chętnie popatrzę

Saizou : tylko się ruszę po książki

zombi: Możecie mi pomóc, bo jestem noga z planimetrii matura z pazdro https://matematykaszkolna.pl/forum/243421.html Też czegoś poszukam to mogę wrzucić za chwilę.

Godzio: No i coś ode mnie: Rozważmy rodzinę prostych przechodzących przez punkt P(0,−1) i przecinających parabolę y =

	1
		x2 w dwóch punktach. Wyznaczyć równanie środków powstałych w ten sposób cięciw
	4

paraboli

Saizou : Oblicz sumę kwadratów odległości dowolnego punktu okręgu o środku O=(0:0) i promieniu r od prostych równoległych do osi układu współrzędnych zawierających boki prostokąta wpisanego w ten okrąg.

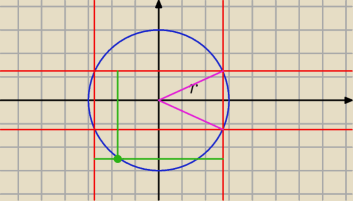
Godzio: Fajne zadanko, musiałem się chwilkę zastanowić. Dobrze rozwiązane? Równanie okręgu: x² + y² = r² Proste poziome: x = m x = − m, m > 0 Proste pionowe: y = a y = −a a > 0 Zależność między m, a i r: m² + a² = r² Suma kwadratów odległości od punktu P(x,y) (y − a)² + (y + a)² + (x − m)² + (x + m)² = 2(x² + y²) + 2(a² + m²) = = 2r² + 2r² = 4r²

zombi: To z kiełbasy chyba, podobne już widziałem.

Godzio: zombi już patrzę na Twoje

Saizou : akurat z Nowej Ery

Maslanek: Pomyliłeś nazwy prostych Cięzka rozkmina się zrobiła

Saizou : wynik r²

Godzio: Ano, poziome powinny być pionowe i na odwrót (y − m)² + (y + m)² + (x − a)² + (x + a)² Ale i tak nie wiem gdzie jest błąd w rozumowaniu

Maslanek: Wydaje się dobrze Jeszcze zanim znałem wynik

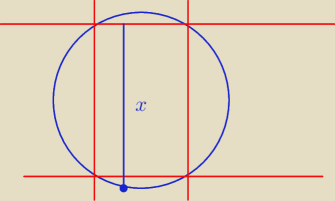
Godzio: Ale wynik r² jest możliwy ? x > r więc x² > r², a jeżeli dodamy inne odległości to już będzie znacznie większa.

Godzio: Maslanek w ogóle co studiujesz, jeśli mogę wiedzieć ?

Saizou : pomyłka 4r², 4 nie zaskoczyła przy wklepywaniu

zombi: Nowa Era ten listek niebieski?

Godzio: Oj zombi ciężkie to zadanie, teraz chyba nie dam rady bo zaraz zasnę

Piotr 10: zombi chcesz odpowiedzi do tego arkusza czy masz je?

zombi: Wydaje mi się, że może pójść przy pomocy tego: http://pl.wikipedia.org/wiki/Twierdzenie_Cevy Zazwyczaj pyka z tego, może nie da się tutaj wykorzystać, nie wiem.

zombi: Nie mam. Btw. Piotr masz może więcej arkuszy pazdro z odpowiedziami ?

Piotr 10: Tak, mam. Chcesz linka ?

Piotr 10: Akurat co robiłem te arkusze, to właśnie ten arkusz jest najtrudniejszy moim zdaniem, wcześniejsze było łatwiejsze

Maslanek: Matematykę stosowaną

	1
Punkty (x,y)=2*(a, a2−		) dla a∊(−∞,−1)∪(1,∞)
	2

Więc x=2a ⇒ x<−2 lub x>2 y=2a²−1 ⇒ y>1

	x
wyznaczając a z pierwszego mamy: a=
	2

	x		x2
I podstawiając do 2: y=2(		)2−1=		−1
	2		2

	x2
Czyli równanie tych punktów, to y=		−1 dla x∊(−∞,−2)∪(2,∞)
	2

zombi: A byłbyś tak miły i rzucił linkiem? Byłbym wdzięczny mega.

Piotr 10: proszę http://tomaszgrebski.pl/viewpage.php?page_id=13

zombi: Wielkie dzięki!

Piotr 10:

Godzio:

Maslanek: Kciuk dla mnie?

Godzio: Tak

Maslanek: Dziękuję Za matmę pewnie

pigor: ..., a ja wrócę do tego : wykazać że jeśli a²+b² ≤ 2 , to a+b ≤ 2, −−−−−−−−−−−−−−−−−− bo chcę mieć w swojej ... szufladzie taki dowodzik : 0 ≤ (a−b)² ⇔ 2ab ≤ a²+b² i a²+b² ≤ 2 ⇒ 4ab ≤ 4 ⇒ ⇒ 2√ab ≤ 2, ale √ab ≤ ¹₂(a+b) ⇒ 2√ab ≤ a+b ≤ 2 c.n.w. . ...

pigor: ..., a dla chętnych może jeszcze np. tak : a²+b²≤ 2 ⇔ a²−1+b²−1 ≤ 0 i niech a²=1+x i b²=1−y, czyli x−y≤ 0 ⇒ ⇒ a=√1+x i b=√1−y i z nierówności √1+x+√1−y≤ 2√¹₂(1+x+1−y) ⇒ ⇒ a+b ≤ 2√¹₂(2+x−y) i x−y≤ 0 ⇒ a+b ≤ 2√¹₂*2=2√1= 2 .

Domel: A można ze średnich? _{______}

	x2+y2		x+y
√		≥		/2
	2		2

x2+y2		(x+y)2
	≥
2		4

	(x+y)2
x2+y2 ≥
	2

Z warunków wstępnych

	(x+y)2
x2+y2 ≤ 2 =>		≤ 2
	2

(x+y)² ≤ 4 => x+y ≤ 2 Czy tak może być?

pigor: ... , właśnie z tych średnich zrobił 3 dni termu 24.03. 21:05 powyżej razor .