plani zombi: Mógłbym prosić jakąś dobrą duszyczkę o wykonanie rysunku? Bo na kartce jakoś mi nie wychodzi. Tylko rysunku, rozwiaze sam. W trójkącie ABC na boku BC zaznaczono punkt D, na boku AC zaznaczono punkt E, na boku AB punkt F. Poprowadzono okręgi o_A, o_B, o_C, w ten sposób, że do okręgu o_A należą punkty A, E, F, do o_B – punkty B, D, F, a do o_C – punkty C, D, E. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.

Godzio: Trochę ciężko to narysować tutaj, ale przedstawie mniej więcej jak to narysować. Narysuj trójkąt ABC. Zaznacz dowolnie punkty E, F, G (oczywiście na odpowiednich bokach). Połącz punkty E,F,G ze sobą. Wykreśl trójkąty opisane na trójkątach AEF, BDF, CDE. Pamiętamy, że środek to punkt przecięcia symetralnych, a je dosyć prosto się wykreśla. Jak nie wiesz to pisz

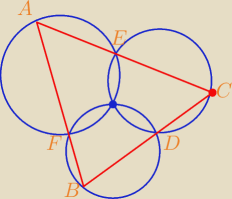
Godzio: A jednak się udało

zombi: DZIĘKI WIELKIE GODZIO WOW JESZCZE RAZ DZIĘKI! DOBRA TO DO ROBOTY.

Godzio: Rysunek bardzo łatwo się rysowało Rysujesz trzy okręgi (tak jak na rysunku, następnie z jednego prowadzisz prostą przez punkt przecięcia dwóch dowolnych i ona Ci przecina drugi okrąg w jakimś punkcie, z niego prowadzisz prostą przez punkt przecięcia dwóch kolejnych okręgów i ostatnia prosta jest już zdeterminowana.

zombi: Szukam tu twierdzenia Cevy, ciekawe czy znajdę

Maslanek: Skoro mamy taki rysunek, to spróbujmy może dorysować okrąg opisany na tym trójkącie (w końcu wierzchołki leżą na poszczególnych okręgach) Albo może inaczej: Gdyby do każdego okręgu dorysować odcinki w trójkącie tak by były opisane na poszczególnych (mniejszych trójkątach). Wtedy może by łatwiej poszło

zombi: Podbitka może ktoś spojrzy.

Vax: Oznacz jakoś przecięcie pewnych 2 okręgów i pokaż, że ten punkt leży też na 3 okręgu.