geometria analityczna tyu: czy ktoś mógłby mi wytłumaczyć jak obliczyć punkt równoodległy od prostej.Sam się tego uczę.

	I Ax0 +By0 + C I
Wzór na odległość punktu P(x0, y0) d=
	√ A2 + B2

Zadanie jest takie Dane są dwie proste k: x−y+3=0 oraz m: 7x+y−1=0 Znajdź na osi OX punkt P rownoodległy od tych prostych.

	Ix + 3I		|7x−1|
No i w tym rozwiązaniu 183590 jest		=
	√2		√50

	I Ax0 +By0 + C I
rozumiem, że stosuje się tutaj wzór d=
	√ A2 + B2

ale dlaczego oblicza się P ( x,0) Skąd wynika te zero we współrzędnych? Czy tutaj pomija się współrzędną y₀, bo ona jest taka sama dla tego punktu ?

lk: Rzędna szukanego punktu wynosi 0 bo jak masz w treści zadania punkt P znajduje się na osi OX.

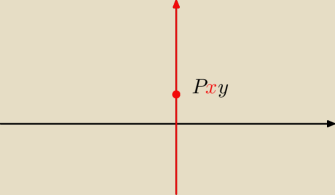tyu: a gdy w następnym zadaniu jest treść "znajdź na osi OY punkt P równoodległy od prostych k i m" to mam przyjąć, ze x₀=0 i pominąć we wzorze tą współrzędną i liczyć tylko y₀. Pytam, bo łatwiej geometrię zrozumieć, jeśli coś można sobie zobrazować, a ja to nie za bardzo "widzę"

lk: dokładnie tak.

tyu: ok dziękuję, trochę się wyjaśniło

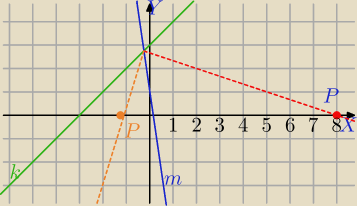Mila: Dane są dwie proste k: x−y+3=0 oraz m: 7x+y−1=0 Znajdź na osi OX punkt P rownoodległy od tych prostych. k: y=x+3 m: y=−7x+1 Punkt P(x,y) ∊OX jednakowo odległy od m i k⇔ P=(x,0) i należy do dwusiecznej kąta między prostymi.

|x−0+3|		|7x+0−1|
	=		⇔
√12+12		√72+12

|x+3|*5=|7x−1|

	7
stąd P=(8,0) lub P=(−		,0)
	6