| 1 | ||
postać kierunkowa k: y= | x, | |
| 2 |
| 1 | ||
x2 −2x +1 + | x2 − 3x + 9 = 9 | |
| 4 |
| 1 | ||
x2 −2x +1 + | x2 − 3x = 0 | |
| 4 |
 w piątek laptop mi się zaczął psuć, więc dałem sobie spokój z internetem
no więc taki mam pomysł na to zadanie.
1/ wyznaczam wzór tego okręgu ze wzoru podanego w treści zadania − zrobiłem to, ale chyba źle
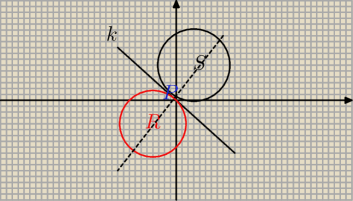
2/ później ustalam w jakim miejscu (np pkt P) jest okrąg styczny z prostą k, która jest osia
symetrii − próbowałem to zrobić, ale delta nie wyjdzie mi jako liczba wymierna, więc x1 i x2
też nie będą liczbami wymiernymi
3/ jeśli znajdę ten punkt styczności P, będzie to środek odcinka łączącego okrąg o środku S z
obrazem tego okręgu o środku np R.
4/ wyznaczam sobie środek tego okręgu R ze wzoru na środek długości odcinka RS
W treści polecenia wkradł się błąd w ostatnim zdaniu. Powinno być "Znajdź równanie obrazu tego
okręgu, a następnie znajdź równania prostych będących osiami symetrii sumy obu okręgów"
Nie wiem co to jest oś symetrii sumy obu okręgów, więc na drugą część polecenia nie mam
pomysłu
Zamieszczam rysunek, ale chyba nie do końca jest on właściwy.
w piątek laptop mi się zaczął psuć, więc dałem sobie spokój z internetem
no więc taki mam pomysł na to zadanie.
1/ wyznaczam wzór tego okręgu ze wzoru podanego w treści zadania − zrobiłem to, ale chyba źle
2/ później ustalam w jakim miejscu (np pkt P) jest okrąg styczny z prostą k, która jest osia
symetrii − próbowałem to zrobić, ale delta nie wyjdzie mi jako liczba wymierna, więc x1 i x2
też nie będą liczbami wymiernymi
3/ jeśli znajdę ten punkt styczności P, będzie to środek odcinka łączącego okrąg o środku S z
obrazem tego okręgu o środku np R.
4/ wyznaczam sobie środek tego okręgu R ze wzoru na środek długości odcinka RS
W treści polecenia wkradł się błąd w ostatnim zdaniu. Powinno być "Znajdź równanie obrazu tego
okręgu, a następnie znajdź równania prostych będących osiami symetrii sumy obu okręgów"
Nie wiem co to jest oś symetrii sumy obu okręgów, więc na drugą część polecenia nie mam
pomysłu
Zamieszczam rysunek, ale chyba nie do końca jest on właściwy.