Okrąg i symetria matt: Okrąg o równaniu x² + y² −2x + 6y + 1 = 0 przekształcono przez symetrię względem prostej k: x−2y =0. Znajdź równanie obrazu tego okręgu, a następnie znajdź równania prostych będących osiami symetrii obu okręgów. Liczę na pomoc i wyjaśnienie, pozdrawiam

Aga1.:

	1
y=		x
	2

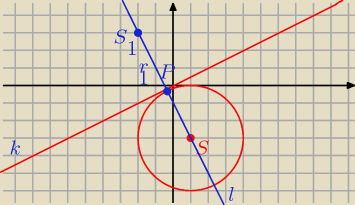
S(1,−3) r=√1+9−1=3 Osie symetrii: to prosta k i prosta l prostopadła do k przechodząca przez S r₁=r=3 Punkt P to punkt przecięcia sie prostych ki l. Znajdziesz go rozwiązując układ równań. Punkt P jest środkiem odcinka SS₁.

matt: Dziękuję, zdążyłem je wymyśleć na inny sposób