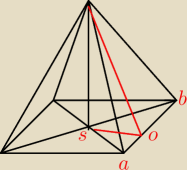
bry Radek: Jeżeli w podstawie ostrosłupa mam romb i mam podną długość boków oraz wysokość ściany bocznej to to żeby wyliczyć H ostrosłupa prowadzę wysokość w trójkacie asb a nie na połowę boku ab ?

Mila: Zgadza się.

...: ... skoro wysokość to prostopadle do podstawy a nie do środka

Radek: to właśnie do tego zadanie to było Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa

Radek: ?

Radek: ?

zawodus: Najpierw policz bok rombu

Marcin: Przekątne w rombie, przecinają się pod kątem prostym

Hajtowy:

	12*16
Pole podstawy ma		= 96
	2

Krawędź podstawy, czyli bok rombu ma: 6² + 8²=100 √100=10 Wysokość ściany bocznej:

4 * 10 h
	= 104
2

40h=208

	208		26
h=		=
	40		5

A wysokość ostrosłupa z pitagorasa

Radek: Ja zrobiłem to zadnie tylko chodzi mi to żeby wyliczyć H ostrosłupa prowadzę wysokość w trójkacie asb a nie na połowę boku ab bok rombu 10

Radek: @Hajtowy nie prosiłem o rozwiązania , zadałem inne pytania a Ty wyjeżdżasz z rozwiązaniem. Policzyłem to zadnie tylko pytam czemu muszę tak a nie inaczej

Mila:

	1
Musisz znać wysokość rombu, |OS|=		h▱.
	2

zawodus: Radek jesteś niegrzeczny. Odpowiedź na twoje pytanie zawiera definicja kąta dwuściennego. Polecam lekturę...

Radek: Ale czemu odpada wersja do środka boku ?

Mila: W − wierzchołek ostrosłupa. ΔABW nie jest trójkątem równobocznym, spodek jego wysokości nie jest środkiem boku AB.

Radek: Nie niegrzeczny tylko pytam cały czas o coś innego.. nie chciałem rozwiązania.

Radek: W ostrosłupach to zawsze działało. A to nie jest promień okręgu wpisanego w romb ?

zawodus: To działało dla ostrosłupów prostych. Ten taki nie jest.

zawodus: To jest promień okręgu wpisanego.

Radek: Wiesz co mietek współczuję osobą w Twoim otoczeniu że muszę z Tobą przebywać.

Radek: czyli tutaj nie działa trik z promieniem ?

Marcin: Radek daj sobie spokój. Szkoda się na niego denerwować Chwila nie zwracania uwagi i odpuści

zawodus: Co dla ciebie znaczy trik z promieniem?

Radek: To że jeśli mam wysokość ostrosłupa i promień okręgu wpisanego to policzę wysokość ściany bocznej ?

mietek: Ja lubię kiedy wy tak denerwujecie na własną niewiedze I olbrzymie ukłony dla osób które chcą "niektórym" pomagać Darmowa pomoc i jeszcze jakie pretensje... Ludzie na korkach płacą grubą kasę za pomoc...

zawodus: Tak

Radek: A piszesz, że w tym wypadku to nie działa ?

zawodus: Bo dokładnie nie mogę cię zrozumieć Krawędzie boczne równe = spodek wysokości w środku okręgu opisanego Kąty nachylenia ścian równe = spodek wysokościw środku okręgu wpisanego W obu przypadkach mamy trójkąty Promień (odpowiedni) okręgu, wysokość ściany bocznej , wysokość ostrosłupa.

Radek: 20:36 chodzi cały czas o to zadanie czy odległość spodka wysokości od krawędzi podstawy to r okręgu wpisanego ?

zawodus: Tak pisałem, że to środek okręgu wpisanego.

Radek: Czyli ten sposób działa jednak

zawodus:

Mila: Tak, ale rysunek jest ważny, bo bierzemy pod uwagę promień okręgu wpisanego w romb, a nie połowę boku.

Radek: Dziękuję o to mi chodziło od początku czyli jeszcze jeśli w podstawie mam inną figurę niż trójkąt równoboczny i kwadrat to promień okręgu opsianego na tej figurze ?

Mila: Nie na każdym wielokącie da się opisać okrąg. Indywidualnie rozważamy problemy.

zawodus: Nie. W zadaniu masz info o tym czy ostrosłup jest prosty czy nie ma jej. Ewentualnie prawidłowy. Wtedy to spodek = środek opisanego Jeśli ściany nachylone pod tym samym kątem= spodek w środku wpisanego. To są podstawowe kryteria Jeśli jej nie ma to może być kwadrat w podstawie a spodek wysokości może leżeć gdzie chce.

Radek: Dziękuję, zrozumiałem.

Radek: Podstawą ostrosłupa ABCDS jest prostokąt ABCD , a krawędź boczna SA jest jego wysokością. Wykaż, że suma kwadratów pól ścian ABS i BCS jest równa sumie kwadratów pól ścian ADS i DCS . Nie wiem jak tutaj zrobić rysunek ?

zawodus: Spójrz na podłogę w pokoju − prostokąt Jeden z rogów pokoju to krawędź prostopadła do podstawy. Łączysz i masz ostrosłup.

Radek: Racja ! Już rysuję.

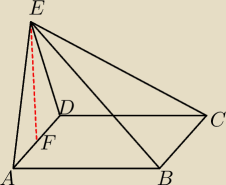
Radek: Podstawą ostrosłupa ABCDE jest kwadrat ABCD . Punkt F jest środkiem krawędzi AD , odcinek EF jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że AE = 15,BE = 17 . OD czego zacząć ? Tutaj nie mogę nic wyliczyć

zawodus: Trójkąty ABE i CDE są prostokątne

Radek: ABE jest prostokątny ?

zawodus: Ściany są prostokątne to i krawędzie też AE jest prostopadły do AB.

Radek: AEF i FDE to tak ?

zawodus: To też trójkąty prostokątne. Dodatkowo trójkąt ADE jest równoramienny.

Radek: Ale ja tam nie widzę kątów prostych

zawodus: Gdzie?

Radek: w tych trójkatach które Ty podałeś

zawodus: Oczywiście chodzi mi o trójkąt AEF a nie kąt AEF. Odcinek EF jest wysokością dlatego jest prostopadły.

Marcin: Musisz to sobie wyobrazić Skoro EF jest wysokością ściany bocznej i jednocześnie wysokością ostrosłupa i jeszcze dodatkowo F jest dokładnie w połowie AD.. Chyba że ja to inaczej widzę

zawodus: Opisz na tej bryle graniastosłup to będziesz lepiej widział kąty proste. Ja idę spać jutro ci zrobię rysunek odpowiedni jak nadal nie będziesz widział

zawodus: Marcin widzisz ok.

Radek: No tak ale ABE i CDE nie są prostokątne

Marcin: Pewnie że są

Marcin: Masz dwa trójkąty prostokątne. Załóżmy że są od siebie oddalone o jakąś odległość. Teraz połącz je ze sobą górnymi wierzchołkami. To że je przechyliłeś, nie zmienia tego, że są nadal prostokątne

Radek: Nie rozumiem tego. To jest z twierdzenie o 3 prostych ?

Marcin: W sumie pierwszy raz słyszę o czymś takim. Musisz sobie to po prostu wyobrazić

zawodus: Albo z twierdzenia. Prosta prostopadła do płaszczyzny jest prostopadła do każdej prostej w niej zawartej.

Mila: Prosta AB jest prostopadła do płaszczyzny w której leży ΔADE i przebija tę płaszczyznę w punkcie A to jest prostopadła do prostej AE przechodzącej przez ten punkt A. Tak samo CD⊥DE.

Radek: Tylko ja cały czas tego nie widzę .

Mila: To korzystaj z tw. Pitagorasa w tych Δ prostokątnych , które widzisz. Obliczysz w ten sposób a.

Radek: Nie wyliczę z tego a bo ja mam tylko jedną daną krawędź

Mila: Dwie.

Mila: A właściwei 4. AE=DE=15 EC=EB=17

Radek: Ale ta jedna nijak ma się do trójkąta AEF

jakubs: z tw pitagorasa policzysz AB. AF to 0,5*AB

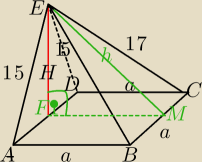
Mila: Załóżmy, że nie widzisz ,że te boczne Δ są prostokątne. 1) W Δ EFM: H²+a²=h² 2) W ΔEMC:

	1		1		1
172=h2+(		a)2⇔289=h2+		a2⇔h2=289−		a2
	2		4		4

W ΔEFA:

	1		1		1
152=H2+(		a)2⇔225=H2+		a2⇔H2=225−		a2
	2		4		4

Podstawiam do (1)

	1		1
225−		a2+a2=289−		a2⇔
	4		4

a²=64 a=8 H=√15²−4²

Radek: Nigdy bym na to nie wpadł, robiłem zadania z forum które Pani dawała innym użytkownikom tzw zadania wprowadzające zrobiłem je wszystkie ale nadal mam poważne problemy z niektórymi zadaniami.

Mila: Zawsze patrz na dane, klasyfikuj Δ, rysuj linie pomocnicze. Pracuj dalej, powinny do maja zniknąć problemy.

zawodus: Warto opanować teorię np.twierdzenie o 3 prostych prostopadłych.

Mila: Ze zrozumieniem.

Radek: Ale książkowa wersja do mnie nie dociera jakoś

zawodus: A jaka jest ta książkowa wersja?

Radek: http://www.matmana6.pl/tablice_matematyczne/liceum/geometria_w_przestrzeni_stereometria/112-twierdzenie_o_trzech_prostych_prostopadlych

zawodus: i w czym jest problem? ładnie przedstawione jest

Radek: Całego tego twierdzenia.

Mila: Zobacz inny sposób rozwiązania zadania z ciągami− masz tam mój sposób i Ety https://matematykaszkolna.pl/forum/242883.html

Radek: Do ciągów i analitycznej wrócę jutro teraz próbuje te bryły