Help. helpless: Potrzebuję pilnej pomocy, będę wdzięczna za wszelkie wskazówki. 1. W ciągu arytmetycznym różnica między pierwszym i piątym wyrazem jest równa 16. Wyznacz wzór ogólny tego ciągu. Oblicz sumę jego 26 wyrazów. 2. Dany jest ciąg o wyrazie ogólnym a_n={2n+1}{3n−1}, wyznacz a_n+2 2. Rozwiąż, przedstaw rozwiązanie na osi i podaj rozwiązanie w postaci przedziału

|2x+11|
	<5.
2

3. Dany jest trójkąt prostokątny. Jedna z przyprostokątnych jest o 6 krótsza od przeciwprostokątnej. Wyznacz długość tej przyprostokątnej jeśli wiadomo, że przeciwległy do niej kąt ostry ma miarę 30 stopni.

wredulus_pospolitus: a czemu potrzebujesz PILNEJ pomocy

helpless: Pilnej, ponieważ muszę je oddać jeszcze dzisiaj. Jest ich więcej, ale większość w miarę mi powychodziła (mam nadzieję), za to w sprawie tych trochę dla mnie trudniejszych postanowiłam skorzystać z internetowej konsultacji. Nie oczekuję pełnych rozwiązań, ale chociaż niech ktoś mnie naprowadzi jak się za to zabrać, bo w sieci jest multum info, ale nie mogę znaleźć nic konkretnego.

	2n+1
W drugim źle się wyświetliło, miało być an=
	3n − 1

wredulus_pospolitus: 2. a_n+2 = .... wszędzie zamiast 'n' wstawiasz 'n+2' to tak jak f(x) = x²+3x+1 to f(x+2) = (x+2)² + 3(x+2) + 1

wredulus_pospolitus: 1. PODSTAWOWY wzór ciągu arytmetycznego: a_n = a₁ + (n−1)*r a więc: a₅ = a₁ + (5−1)*r = a₁ + 4r (logiczne, prawda ?!) a więc: a₅ − a₁ = 4r = (dane w zadaniu) 16 stąd r = .... w takim razie: a_n = ... wzór ogólny z podstawionym już 'r' A czy tutaj nie było gdzieś podanego a₁

wredulus_pospolitus: 2. nierówność: zapoznaj się z: https://matematykaszkolna.pl/strona/1653.html

J: Brakuje danych

helpless: Dziękuję Panu za pomoc! ; ) No w tym rzecz, że właśnie nie było, tylko ta różnica między wyrazami.

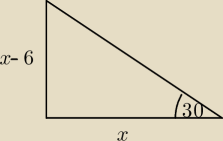
wredulus_pospolitus: 3) patrz rysunek skorzystaj z odpowiedniej funkcji trygonometrycznej i rozwiąż równanie

wredulus_pospolitus: autorko ... BZDUUURA

helpless: Wiem mniej więcej jak to jest z nierównościami, ale nie mogę znaleźć żadnego przykładu podobnego w budowie do tego, który muszę rozwiązać. Najpierw muszę pomnożyć obustronnie przez 2, żeby pozbyć się kreski ułamkowej czy wylicza się to jakoś inaczej? Wtedy po drugiej stronie byłoby 10 i biorąc pod uwagę wartość bezwzględną muszę dopisać jeszcze drugie rozwiązanie − z przeciwnym znakiem (>) i −10 i po prostu wyliczyć oba x?

wredulus_pospolitus: najprościej to zaznaczyć na osi OX

J: I2x +11I < 10 ⇔ −10 < 2x + 11 < 10 ⇔ −21 < 2x < −1 ⇔ x ∊ ( −21,−1)