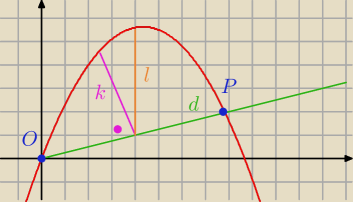
Rakieta Saizou : Siemka ludziska mam pytanie do zadania Przyjmijmy układ współrzędnych następująco: oś Ox równoległe do poziomu morza, oś Oy pionowa. Rakieta wystrzelona z punktu O porusza się w tym układzie po paraboli t=−0,016x²+1,6x (x[km]). Teren od punktu O wznosi się w górę , a jego wysokość na poziomem morza zmienia się

	1
według zależności y=		x (x[km]).
	5

a) oblicz w tym układzie współrzędne punktu, w którym rakieta spadnie na ziemię oraz odległość d tego punktu od startu (z dokładnością do pełnych km.) b) Jaką maksymalną wysokość h (w pionie) od powierzchni ziemi osiągnie ta rakieta? (z dokładnością do pełnych km) podpunkt a nie stanowi problemu P(87,5; 17,5) d≈89 km a w podpunkcie b odległość liczona w pionie od powierzchni ziemi to odcinek k czy l

ICSP: https://matematykaszkolna.pl/forum/241376.html

Saizou : ICSP pamiętam, ale teraz mam inne sprawy na głowie

Saizou :

Ajtek: Witam Saizou, ICSP . Wg mnie to będzie l, ale ręki sobie nie dam uciąć.

Saizou : a ja uważam że k, bo ma być "(w pionie) od powierzchni ziemi " czyli wg mnie prostopadle od

	1
prostej y=−		x
	5

Saizou : ktoś jeszcze się wypowie

Ajtek: A może i masz rację .

Saizou : sam nie wiem, dlatego się pytam mądrzejszych ode mnie

Ajtek: Jak widzisz, wcale mądrzejszy nie jestem .

Saizou : ktoś się wypowie Eta, Mila, Domel, ICSP, Krzysiek, Mateusz, zombi, Vax, Jakub, Piotr10 ktokolwiek ?

Saizou : jesteś, jesteś...

Saizou : up?

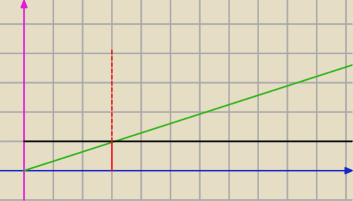
Ajtek: A czy to nie jest tak, że poziom ziemi w punkcie x₀ odpowiada poziomowi morza?

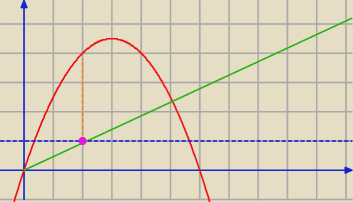
Ajtek: Zły rysunek zrobiłem.

Domel: 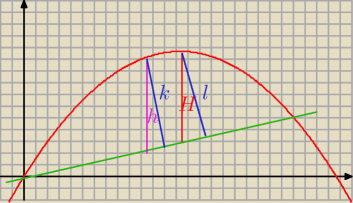Saizou wg mnie największa odległość od gruntu to h h > H, h > k, h > l h(x) = t(x) − y(x) = −0,016x² + 1,6x − 0,2x = −0,016x² + 1,4x

	1,4
xmax = −		= 43.75
	2*(−0,016)

	1,96
hmax = −		= 30,625
	4*(−0,016)

a w wierzchołku paraboli (x_w = 50 => h_w = 30)

wredulus_pospolitus: A ja chciałbym się przyczepić do pewnej sprawy −−− nie została uwzględniona krzywizna Ziemi (co przy takiej odległości już powinno się uwzględniać) a co do tego (b) ... prawidłowa odległość (jeżeli nie patrzymy na krzywiznę Ziemi) to będzie l ponieważ ta prosta 'przechodzi' przez jądro planety = jest w pionie Gdyby była uwzględniona krzywizna planety, to by nie było problemu ... w końcu pion w danym punkcie = prosta od środka kuli do tegoż punktu.

Maslanek: Może dodatkowa argumentacja jeszcze z mojego punktu widzenia Wykres ten przedstawia y(x)? Jeżeli tak, to y−położenie n.p.m w dowolnym punkcie. Więc h − wysokość nad ziemią będzie dana wzorem h(x)=y₁(x)−y₂(x) (gdzie y₁, y₂ odpowiednie funkcje)

Saizou : dziękuję wszystkim za pomoc