Czworokąty EMPE: Na trapezie o podstawach długości 16cm i 8cm oraz wysokości 8cm opisano okrąg; jego środek leży wewnątrz trapezu. Oblicz odległość środka okręgu od wszystkich boków tego trapezu.

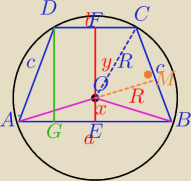
Mila: a=16 b=8 h=8 x+y=8 EB²+x²=R² 8²+x²=R²⇔x²+64=R² FC²+y²=R² 4²+y²=R²⇔y²+16=R² x²+64=y²+16 x²−y²=−48 (x−y)*(x+y)=−48⇔(x−y)*8=−48 x−y=−6 x+y=8 2x=2 x=1 i y=7 R²=1²+64 R=√65 AG=(16−8):2=4 W ΔAGD: c²=4²+8²⇔c²=80⇔c=4√5 W ΔBMO: OM²+(2√5)²=R²⇔|OM|²+20=65 |OM|=√45 |OM|=3√5 Odległości; Od AB to1 Od DC to 7 Od BC i od AD to 3√5

Eta: https://matematykaszkolna.pl/forum/156352.html