Proszę o pomoc ( geometria)
AmD: na trapezie o podstawach długości 16 cm i 8 cm oraz wysokości 8 cm opisano okrąg. jego środek
leży wewnątrz trapezu. oblicz dl długości środka okręgu od wszystkich boków tego trapezu.
23 wrz 22:03
AmD: up
23 wrz 22:15
sushi_gg6397228:
za zadanie trzeba było się zabrać 48h temu. Przepisanie gotowca teraz a przed lekcją == efekt
taki sam
23 wrz 22:20
AmD: ale za to bede chociaz wiedzial jak zrobic takie zadanie

23 wrz 22:27
ale urwał: Trapez ABCD. S − środek okręgu opisanego E − środek AB, |EB| = 8 G − środek BC, |BC| = √82 + 42
= 4√5, |GB| = 2√5, F − środek CD, |CD| = 4 |SB| = |SC| = R − długość promienia okręgu
opisanego na trapezie, |SF| = y, |SE| = x, |SG| = z Z tw. Pitagorasa: 1. w Δ FSC: x2 + 42 = R2
2. w Δ ESB: y2 + 82 = R2 3. w Δ GSB: z2 + (2√5)2 = R2 oraz 4. x + y = 8 Rozwiązując ten uklad
równań (1., 2., 3., 4) otrzymujemy: x = 7, y = 1, z = 3√5
23 wrz 22:33
ale urwał: to by było na tyle przepraszam,że tak chaotycznie − już jest późno
23 wrz 22:37
Eta:
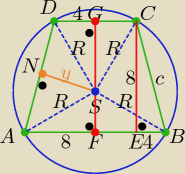
|SF|=x i |SG|= 8−x
R
2= 8
2+x
2 i R
2= 4
2+(8−x)
2
to: 64+x
2 = 16+64−16x+x
2 ⇒ ...... x=1
|SF|=1 i |SG|= 7
to: R
2= 65 ⇒ R=
√65
c
2=8
2+4
2 ⇒ ............. c= 4
√5
z tw. Pitagorasa w ΔASN wyznacz |NS|=y=......
i po ptokach

23 wrz 22:46
ale urwał: Eta wynik już jest u góry chyba dobrze jest

mianowicie x = 7, y = 1, z = 3√5
23 wrz 22:50
Eta:
Jak pisałam i rysowałam, nie widziałam Twojego wpisu

23 wrz 22:52

 |SF|=x i |SG|= 8−x
R2= 82+x2 i R2= 42+(8−x)2
to: 64+x2 = 16+64−16x+x2 ⇒ ...... x=1
|SF|=1 i |SG|= 7
to: R2= 65 ⇒ R= √65
c2=82+42 ⇒ ............. c= 4√5
z tw. Pitagorasa w ΔASN wyznacz |NS|=y=......
i po ptokach
|SF|=x i |SG|= 8−x
R2= 82+x2 i R2= 42+(8−x)2
to: 64+x2 = 16+64−16x+x2 ⇒ ...... x=1
|SF|=1 i |SG|= 7
to: R2= 65 ⇒ R= √65
c2=82+42 ⇒ ............. c= 4√5
z tw. Pitagorasa w ΔASN wyznacz |NS|=y=......
i po ptokach 
 mianowicie x = 7, y = 1, z = 3√5
mianowicie x = 7, y = 1, z = 3√5
