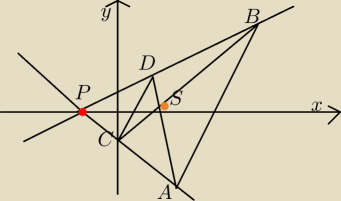
jednokładność tyu: Czy ktoś mógłby mi sprawdzić zadanie, bo chyba w odpowiedziach jest błąd (już drugi, który znalazłem). Zaznaczam, że uczę się tego sam, bez nauczyciela, dzięki Wam i internetom. Wczoraj tłumaczył mi to PW, ale dopiero dzisiaj wszystko zatrybiło (tak mi się wydaje). Treść: "sprawdź, czy odcinki AB i CD są jednokładne. W przypadku odpowiedzi twierdzącej wyznacz środek S i skalę k jednokładności, w której obrazem odcinka AB jest odcinek CD. A (2,−3), B(5,6), C(0,−1), D(1,2)." Ja tutaj oznaczyłem przez punkt S i przez punkt P dwa środki jednokładności, żeby mi się nie myliło, jak będę liczył. W odpowiedziach jest tylko S, które oznacza dwa różne punkty. −−−− Są dwa warianty rozwiązania. Pierwszy wariant. AB^→=[3,9] CD^→=[1,3], są one równoległe, bo k=3. Obrazem punktu C jest punkt A, środkiem jednokładności jest punkt P (a,b) Obrazem punktu D jest punkt B, środkiem jednokładności jest punkt P (a,b) Tworzę układ równań. [2−a,−3−b] = k[0−a,−1−b] [5−a,6−y] = k[1−a, 2−b] [2−a,−3−b] = [−ak,−k−bk] [5−a,6−y] = [k−ak, 2k−bk] 2−a=−ak => 2−a=−ak / (−1) = > −2+a=+ak => k=3 −3−b = −k−bk 5−a = k−ak 5−a = k−ak 5−a = k−ak 6−y = 2k−bk po podstawieniu wszyło mi: a=−1, b=0. Czyli środek jednokładności P(−1,0), skala jednokładności to k=3.

	1
W odpowiedziach jest S(−1,0), k=		. To jest chyba błędna skala k? Bo gdyby była
	3

prawidłowa, to punkt B byłby bliżej od punktu D, a punkt A byłby bliżej od punktu C. To widać też z rysunku. Drugi wariant wyszedł mi tak jak w odpowiedziach. Obrazem punktu A jest punkt D, środkiem jednokładności jest punkt S (a,b) Obrazem punktu B jest punkt C, środkiem jednokładności jest punkt S (a,b)

	5		3		−1
S(		,		), k =
	4		4		3

wredulus_pospolitus: w pierwszym .... obrazem odcinka AB ma być CD więc z większego większego robisz mniejszy ... stąd skala k<1 na pewno

	|AB|
po prostu policzyłeś:		= k .... a winno się na odwrót
	|CD|

wredulus_pospolitus: przypomnij sobie o czym mówi skala 1) znak skali pokazuje 'po której stronie' od środka jednokładności znajduje się obraz 2) wartość skali (z dokładnością do znaku +/−) oznacza czy OBRAZ będzie powiększony (gdy k>1), nie zmieniony (k=1) czy zmniejszony (k<1) ... u Ciebie jest zmniejszony rozmiar

tyu: no dobrze,

	1
a gdzie będzie środek jednokładności, skala będzie w pierwszym wariancie k=		?
	3

Bo moim zdaniem nie będzie to punkt P (−1,0), którego współrzędne się zgadzają z odpowiedziami.

wredulus_pospolitus: punkt dobrze P(−1,0) ... przecięcie prostych

tyu: mi wyszła skala k=3, bo PA^→= k PC^→ PB^→= k PD^→ Trzeba wziąć pod uwagę też gdzie jest środek jednokładności w tym przypadku, czyli od jakiego miejsca "odkłada" się te wektory. Tak myślę, ale nie jestem pewien, dlatego pytam.

wredulus_pospolitus: o skalach: https://matematykaszkolna.pl/strona/902.html

tyu: czyli jeśli środkiem jednokładności jest P(−1,0), to bierzesz wektor o długości PC, "zaczepiasz" go w punkcie P i po prostej, które przechodzi przez punkt P i C, odkładasz trzy

	1
długości i wtedy masz punkt A (2,−3). Jeśli skala jest k =		, to wektor równy
	3

trzeciej części odcinka PC zaczepiasz w punkcie P i odkładasz na prostej, które przechodzi przez punkt P i C, czyli gdyby

	1
skala k =		, to A byłby bliżej niż punkt C
	3

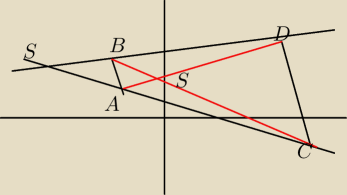
tyu:

	1
czy ktoś mógłby algebraicznie mnie przekonać, że w pierwszym wariancie k=		, bo na
	3

"teorię", to można się spierać godzinami. Wiem, że to trochę liczenia, ale ja tak to rozumiem. W książce jest taki rysunek współrzędne punktów podane w książce jako przykład A(−1,1) B(−2,5) C(8, −2) D(6,6) no i potem jest napisane "SC^→ = k SA^→ SD^→ = k SB^→ " czyli tutaj też "zaczepiasz" w punkcie S odcinek równy np SA odkładasz go k razy (w tym przypadku k=3) na prostej, która przechodzi przez punkty S i A, no i masz punkt C, .

tyu: w zadaniu rozwiązanym w książce zamiast każdy środek jednokładności oznaczyć różnymi literami oznaczono je tak samo, czyli literą S, ale mi się wydaje, że w zapisie "SC^→ = k SA^→ SD^→ = k SB^→ " chodzi o ten punkt S z lewej strony

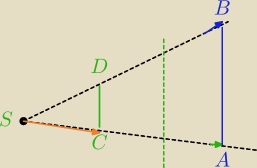
Mila: Zadanie 1. CD=J^k_S(AB) odcinek CD jest obrazem odcinka AB w skali k względem punktu S

	1
Odcinek |CD|=		|AB|
	3

	1		1
W takim razie odcinek AB został przekształcony w skali k1=		albo w skali k2=−
	3		3

Chodzi o to, że skala może byc dodatnia albo ujemna. A (2,−3), B(5,6), C(0,−1), D(1,2).

	1
1) k=
	3

Z definicji jednokładności : C=J^1/3_S(A) Niech S=(a,b)− środek jednokładności:

	1		1
SC→=		SA→⇔[0−a,−1−b]=k*[2−a,−3−b]⇔[−a,−1−b]=		[2−a,−3−b]⇔
	3		3

[−3a,−3−3b]=[2−a,−3−b]⇔a=−1, b=0 S=(−1,0)

	−1
2) k=		w następnym wpisie
	3

C=J{−1/3)(B)⇔ niech P=(p,q)− środek jednokładności:

	−1		−1
SC→=		SB→[0−a,−1−b]=k*[5−a,6−b]⇔[0−a,−1−b]=		*[5−a,6−b]⇔
	3		3

	5		3
[3a,3+3b]=[5−a,6−b]⇔a=		, b=
	4		4

	5		3
P=(		,		)
	4		4

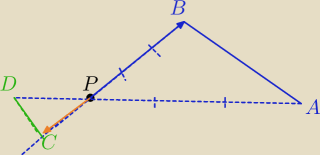
Mila: W trzeciej od dołu, zapisałam dla S (a,b) zamiast P (p,q)

	−1
PC→=(		)*PB→
	3

tyu: już wiem, gdzie zrobiłem błąd. Ja przyjąłem − błędnie − że obrazem punktu C jest punkt A, oraz obrazem punktu D jest punkt B. Skoro polecenie mówi "sprawdź, czy odcinki AB i CD są jednokładne. W przypadku odpowiedzi twierdzącej wyznacz środek S i skalę k jednokładności, w której obrazem odcinka AB jest odcinek CD" to trzeba liczyć w wariancie pierwszym, że obrazem punktu A jest punkt C oraz obrazem punktu B jest punkt D.

	1
Teraz skala mi wyszła		, czyli poprawnie. Zwracam honor wredulus pospolitus i
	3

dziękuję wszystkim.

Mila: