planimetria muflon: 3 okręgi o promieniach 2,4,6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu przechodzącego przez pkt stycznośći tych okręgów.

muflon: środki boków nie mogą tworzyć trojkata, 12=8+4

muflon: jaki przypadek należy teraz rozważyć?

wredulus_pospolitus: jakich boków

muflon: przepraszam, środki okręgów nie mogą tworzyyć troojkata

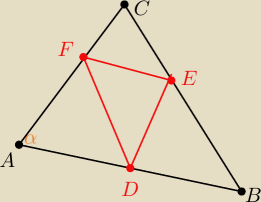
wredulus_pospolitus: należy zauwążyć, że: ΔAFD ≈ ΔABC ... stąd wyznaczasz |FD| analogicznie pozostałe boki ΔDEF następnie odpowiedni wzór na wyznaczenie promienia okręgu opisanego na tymże trójkącie oczywiście A,B,C to środki tych trzech okręgów

J: A niby dlaczego nie mogą ?

muflon: jednak mogą, przecież 2+4=6 4+6=10 6+2=8

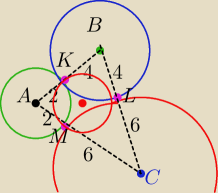Mila: Punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołków kąta. Widać, że punkty : K,L,M spełniają ten warunek, okrąg przechodzący przez te punkty jest okręgiem wpisanym w ΔABC ΔABC ma boki: 6,8 ,10 , zatem jest to Δ prostokątny, ∡A=90^o⇒ r=2 Jeśli tego nie "widzisz", to Skorzystaj z wzoru:

	a+b+c
PΔ=		*r
	2

	1
PΔABC=		*6*8
	2

	6+8+10
⇔24=		*r
	2

Mila: ?

Domel: Mila help https://matematykaszkolna.pl/forum/241380.html