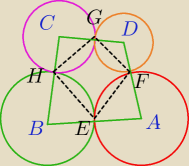
planimetria bezendu: Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg. Wskazówkę proszę jak zacząć.

Mila: Połączyć środki okręgów, to jeden czworokąt. Połączyc punkty styczności to drugi czworokąt. Wykazać, sumy kątów przeciwległych maja po 180^o.

bezendu:

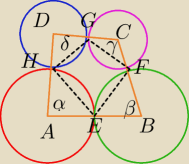
Mila: Oznacz kąty w zielonych narożach, przy podstawach.

bezendu:

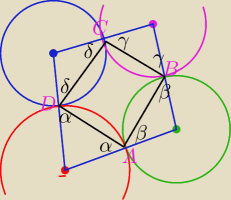
Mila: ∡A=180−(α+β) ∡C=180−(δ+γ) Licz dalej i oblicz sumy. Ma wyjść: ∡A+∡C=∡B+∡D

bezendu: ∡B=180−(β+γ) ∡D=180−(α+δ) Tylko skąd wiadomo jak te kąty są rozmieszczone ?

Mila: Z rysunku i z tego, że masz tam 4 Δ równoramienne. Wreszcie z sumy kątów w czworokącie.

bezendu: Racja, głupi ja nigdy tego nie zauważam..

Mila: Kto pyta ten nie błądzi.

bezendu: Ale czy ja nie za dużo pytam ?

Mila: Nie wygłupiaj się, bo wejdzie tu znana nam osóbka.

bezendu: O tego to bym nie chciał.

bezendu: W kąt o mierze x wpisano ciąg kół w taki sposób, że pierwsze koło ma promień r i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.

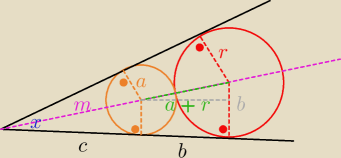
Maslanek: Pytanie, które trzeba sobie zadać jaki promień ma kolejny okrąg? Spodziewamy się, że długości będą tworzyły ciąg geometryczny (nieskończony) Jako, że rozpatrujemy przypadek (ogólny) dla okręgu o promieniu r, to rzeczywiście otrzymamy ciąg geometryczny Jak widzimy środki leżą na dwusiecznej kąta x. To szare b: Z twierdzenia Pitagorasa: (a+r)²=(r−a)²+b² Z twierdzenia Talesa:

m		m+a+r
	=
a		r

c		b+c
	=
a		r

−−−−−− Te trzy równania na pewno wystarczą. Ale pewnie można łatwiej

Mila: Raczej porzuć to zadanie, c. g o wrednym q.

Maslanek: Eh... Oczywiście, że mozna łatwiej, kiedy ma się podany kąt x

	x		a
sin		=
	2		m

Oraz z twierdzenia Talesa:

m		m+a+r
	=
a		r

bezendu: Wrócę do niego po maturze, może wredne ale widziałem w arkusz.

bezendu: Ramiona kąta o mierze 60⁰ przecięto prostą k prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej k . Oblicz stosunek pól tych kół. Tylko wskazówkę

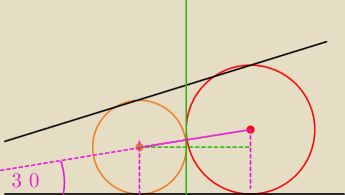
Maslanek: Mam nadzieję, że widać co się wydarzyło

	R
Oblicz stosunek		.
	r

Maslanek: Albo podobnie jak tamto, albo z trochę innych równości możnaby skorzystać Ale wykorzystanie to samo

bezendu: dobra już starczy tych wskazówek

Maslanek: Dobra... Bez sensu to jest −,− Zły jest ten rysunek

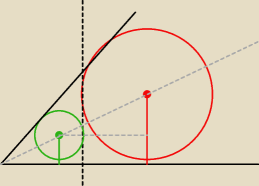
Maslanek: Jeszcze raz, tylko w lepszej skali Ale takie coś może zadziałać ładnie

Maslanek: ONe teraz nie są styczne, tamte były

bezendu: No właśnie

Eta:

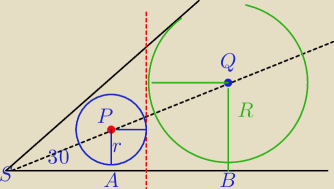
Mila: Te okręgi nie są styczne do siebie tylko do ramion kąta i do prostej prostopadłej. |SP|=2r |AQ|=2R Szukaj zależności:

r
	to będzie skala podobieństwa.
R

bezendu: Czemu |SP|=2r ? a nie r+x |AG|=R+r+x ?

Maslanek: sin 30

Mila: ΔSAP to połowa Δ równobocznego, albo jak u Maslanka.

Mila: |PQ|=2R−2r Oblicz PQ na inny sposób. M − punkt przecięcia protej i dwusiecznej , z tych małych trójkącików oblicz PM i MQ

bezendu: Teraz idę na kolację jak wrócę to spróbuję.

Mila: Wtaj Eta, masz jakiś sposób na q niezbyt wymyślne, czy nie liczyłaś. Nie pisz rozwiązania tylko odpowiedz. Kiedyś to już liczyłam.

Mila: Oczywiście mam na myśli zadanie z 20:38.

bezendu: z tym podobieństwem mam ciężko ruszyć

Eta: Witaj Mila O które zadanie pytasz?

Mila: ETo, z godziny 20:38 z ciągiem geometrycznym w tle. Nie chce mi się dzisiaj liczyc tego. Jutro policzę. Bezendu tam tylko funkcje tryg. w tych małych trójkącikach.

bezendu: Chciałbym sam dokończyć to zadania, ale już dziś nie dam rady. Dziękuję za pomoc i dobranoc.

Mila: Dobranoc, jutro czekam na zakończenie.

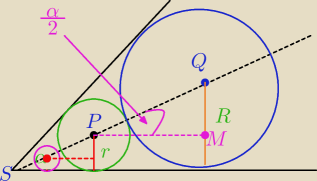
Mila: Zadanie dla Bezendu. W kąt o mierze x wpisano ciąg kół w taki sposób, że pierwsze koło ma promień r i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu. QM=R−r WΔPMQ: |PQ|=r+R

	α		QM
sin		=
	2		PQ

	α
|PQ|*sin		=R−r
	2

	R−r		R−r
|PQ|=		⇔		=R+r
	α   sin   2		α   sin   2

	α		α
R−r=sin		R+r*sin
	2		2

	α		α
R−sin		*R=r+r*sin
	2		2

	α		α
R(1−sin		)=r*(1+sin		)
	2		2

r		α   (1−sin )   2
	=
R		α   (1+sin )   2

Analogicznie :

r'		α   (1−sin )   2
	=
r		α   (1+sin )   2

promienie to kolejne wyrazy c. geom

	α   (1−sin )   2
q=		i |q|<1
	α   (1+sin )   2

Pozostaje obliczyć: S_kół=P₁+P₂+P₃+..... P₁=πR² P₂=π*(Rq)²=πR²*q² P₃=π*(Rq²)²=π*R²*q⁴ S_kół=πR²*(1+q²+q⁴+.....) q₁=q²

	1
Skół}=πr2*
	1−q2

Podstaw i doprowadź do najprostszej postaci.

zawodus: tutaj macie pewne rozwiązanie.. http://www.zadania.info/4263941

zawodus: "pewne" nie znaczy, że Mila ma źle złe sformułowanie

bezendu: Mila dziękuję za rozwiązanie do tego zadania.

Mila: Przeanalizowałeś?

zawodus: Ale cię męczy ten dzieciak

bezendu: Tak, ale to bardzo trudne zadania jak dla mnie.

Mila: To prawda ,trudne.Takiego nie będzie na maturze, ale po próbnych dla klas II wyciągam wnioski, ze matura w tym roku nie będzie łatwa.

Mila: Zawodus, przynajmniej jeden (z niewielu) ambitny.

bezendu: Czasami jednak wole trudniejsze zadania niż prostsze ale nie w przypadku planimetrii.

bezendu: A gdzie mogę znaleźć zadania dotyczące kąta środkowego, wpisanego ? Te na matematyka.pisz już przerobiłem. ?

Mila: http://www.matemaks.pl/playlista.php?id=192

bezendu: Dziękuję już się za nie zabieram. A jest takie jak coś ''kąt dopisany'' ?

omi: https://matematykaszkolna.pl/forum/208849.html

omi: http://www.youtube.com/watch?v=E9c_CyyA-l4

omi: https://www.google.pl/search?q=k%C4%85t+dopisany&rlz=1C2ASUT_plPL444PL456&tbm=isch&tbo=u&source=univ&sa=X&ei=lHMfU4zoJe_Z4QSMiYHACg&sqi=2&ved=0CCcQsAQ&biw=1280&bih=620

bezendu: Dziękuję Eta

Mila: Metamorfozy Ovidiusza?