wyk Radek: Wyznacz wszystkie wartości parametrów a,b , dla których nierówność (x²−x−2)(x²−2ax+3bx−6ab) ≥ 0 jest spełniona przez każdą liczbę rzeczywistą. Proszę o wytłumaczenie co mam zrobić a nie pisanie gotowców ! Z pierwszego nawiasu policzyłem x=−1 x₂=2

Bizon: ... iloczyn dwóch ujemnych .....dodatnia ... iloczyn dwóch dodatnich ... dodatnia Zatem skoro ma być ≥0 dla x∊R ... to

Radek: Nie bardzo rozumiem co mam zrobić z drugim nawiasem ?

Radek: ?

J: Dokładnie to, co napisał "Bizon".Albo obydwa nawiasy ≥ 0, albo obydwa ≤ 0.

Bizon: ... to włącz myślenie ... Masz iloczyn dwóch wielomianów kwadratowych. Ma on być ≥0 dla x∊R Przebieg (wykres) pierwszego znasz ... wiesz gdzie przyjmuje on wartości ujemne a gdzie dodatnie. To jak ma przebiegać ... jaki ma być ten drugi aby zachodziło ... iloczyn dwóch ujemnych .....dodatnia ... iloczyn dwóch dodatnich ... dodatnia i w sumie ≥0 dla x∊R

Radek: Czyli z drugiego mam wyliczać x₁ oraz x₂ ?

Bizon: ... nie policzysz bo masz parametry Masz odpowiedzieć jakie one mają być

bezendu: Jak to nie policzy jak policzy x₁=−3b x₂=2a

pigor: .., co masz zrobić proste; zajrzeć do odpowiedniego działu lub paragrafu podręcznika, to tam znajdziesz np.to, że iloczyn wyrażeń , funkcji , ..., itd : f * g ≥ 0 ⇔ (f ≥ 0 i g ≥0) v (f ≤ 0 i g ≤0) ...

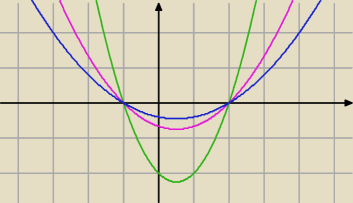
Bizon: coś Ci to mówi ? Teoretycznie mogłyby być takie Ale skoro oba przy x² mają 1 ... to

Radek: ?

Radek:

Marcin: Radku czego nie rozumiesz? Jeżeli x²−x−2≥0, to x²−2ax+3bx−6ab≥0 Jeżeli x²−x−2≤0, to x²−2ax+3bx−6ab≤0 W inny przypadku wyjdzie Ci liczba ujemna.

Radek: Co mi da ten drugi nawias ?

Mila: Wniosek: obydwa trójmiany muszą mieć jednakowe miejsca zerowe, obie parabole są skierowane do góry. Rozwiąż warunek dla trójmianu: W(x)=x²−2ax+3bx−6ab W(−1)=0 i W(2)=0 Wtedy ustalisz a i b.

Radek: A tutaj pisali coś innego ? Dla Pani

Mila: Dziękuję za kwiatka, zrób , co Ci podpowiedziałam, potem będziemy wyjaśniac dalej .

Radek: −1 −3b 2 2a −1=−3b 2=2a 3b=1 a=1

	1
b=
	2

−1=2a 3b=−2

	1		2
a=−		b=−
	2		3

Mila: Pomyliłeś się w pierwszym , ale dobrze zacząłeś.

	1
b=		to a=1
	3

lub

	−2		−1
b=		to a=
	3		2

I to już koniec zadania.

Radek: Będzie Pani jeszcze na forum? Bo ostatnio mnie nie było i chce trochę nadrobić z Pani pomocą

Mila: Jeszcz kilka minut będę.

Radek: Uzasadnij, że jeżeli liczby niezerowe a,b,c spełniają warunek a³+b³=2c to

1		1		2
	+		=
a2+ac+c2		c2+cb+b2		a2+ab+b2

Radek: ?

Radek:

Wazyl: (a+b)(a²+ab+b²)=2c

	2		a+b
P=		=
	a2+ab+b2		c

	a−c		c−b
L=		+
	a3−c3		c3−b3

Dalej sam!

Radek: Napisałeś prawie gotowca o którego nie prosiłem i jeszcze w dodatku nic z tego nie zrozumiałem

Wazyl: Nie napisałem Ci gotowca. Sam nie wiem czy coś z tego będzie (powinno) tylko to mi pierwsze do głowy wpadło. Wyjaśnienie: korzystałem ze wzorów skróconego mnożenia a³+b³=... i a³−b³. PS Czasami lepiej podziękować albo chociaż nie negować jak ktoś wchodzi, czyta Twoje zadanie i poświęca dla Ciebie swój czas. O gotowca nie prosiłeś, gotowca nie dostałeś.

Uczę się: Wazyl zły znak we wzorze skróconego mnożenia.

Radek: To trzeba było napisać wyjaśnienie. Ciekawe czy Ty byś zrozumiał jak ja bym w zadaniu napisał Ci coś a Ty byś nic z tego nie wiedział.

Wazyl: I jeszcze źle CI napisałem z tego wszystkiego i cały pomysł poszedł w diabli. Mam błąd rąbnąłem się w znaku: a³+b³=(a+b)(a²−ab+b²) Czyli zaczynasz od zera.

Uczę się: Radek spokojnie. Według mnie najlepszą nauką jest analizowanie gotowego zadania, a potem robienie podobnych już sam, ewentualnie z jakąś pomocą, więc zdanie wazyla się liczy i jest mocno pomocne.

Wazyl: Radku drogi. Wydaje mi się że jesteś juz dużym chłopcem i nie trzeba Ci wszystkiego pokazywać krok po kroku, tym bardziej że są to wzory skróconego mnożenia które musisz znać na maturę. Zrozumieć nie wiem czy bym zrozumiał ale na pewno popatrzyłbym na to i zastanowił się jak to wyszło. Dobranoc

Radek: A ja wolę wskazówkę i sam chcę dojść do rozwiązania. i tak się najlepiej uczę, gotowce mogę znajdować na internecie.

Wazyl: Ogarnij się chłopie nie napisałem Ci gotowca poza tym to co napisałem jest ŹLE. Sam se rozwiązuj swoje zadania

5-latek: Przy takim postepowaniu Radka to nie wiem kto zostanie mu do pomocy kazdy sie bedzie bal cos napisac bo nie bedzie wiedzial czy to gotowiec czy wskazowka by sie nie narazic na krytyke z jego strony

Uczę się: To wskazówka jest taka, że zapewne te a³+b³=2c musisz zamienić na coś takiego co jest w którymś z mianowników. jesteś pewien że dobrze przepisałeś zadanie?

Radek: Tak dobrze przepisałem.

Radek: Przy takim postępowaniu ? Bo co bo nie chcę dostawać gotowców ? Bo wole sam pomyśleć niż wpisać tylko wynik ? I nie wiem czemu Pan to pisał skoro to mi nie pomaga akurat w rozwiązaniu mojego zadania...

jakubs: Ja bym radził iść spać. I rano podejść do tego zadanka od początku jeszcze raz.

5-latek: Radku nie dostales gotowca Po drugie . Sledze Twoje posty (tak) i zawyczaj prosisz o wskazowki a na koncu okazuje sie ze i tak dostajesz gotowce . I na tym to zakonczmy . Zycze przyjemnego rozwiazywania zadan . Naprawde

zawodus: Zadanie, nie jest poprawnie sformułowane niestety. Podana równość nie zachodzi.

Radek: I nadal nie mogę dojść do poprawnego rozwiązania

Mila: Czy nie powinno być ( 2c³) z prawej strony?

Radek: Powinno

Mila: No to rozwiązuj teraz, podpowiem:

m3−n3		(m−n)*(m2+mn+n2)
	=		=(m2+mn+n2)
(m−n)		(m−n)

Możesz spróbować wykorzystać.

Radek:

	(a−b)		(c−b)
L=		+
	(a−b)(a2+ab+b2		(c−b)(c2+cb+b2

Mila: Z lewej masz w obu wyrażeniach c. Popraw i skorzystaj z założenia.

Radek:

	(a−c)		(c−b)
L=		+		=
	(a−c)(a2+ac+b2)		(c−b)(c2+cb+b2

	(a−c)		(c−b)
L=		+		?
	a3−c3		c3−b3

Mila: Teraz oblicz z danych (c³) i podstaw w mianowniku.

Radek: Dziękuję już dokończyłem a teraz pytania jak mająć Sumę ciągu arytmetycznego S_n=n²+5n wyznaczyć a₁ ?

5-latek: a₁=S₁

Radek: a skąd taka zależność ?

5-latek: ze wzoru na wyraz a_n = S_n−S_n−1

mietek: Radek myślenie to ty w gimnazjum zostawiłeś ... Dobrze, że da się na pamięć tego nauczyć....

5-latek: lub tez a_n=S_n+1−S_n

mietek: drugi bardziej mnie się podoba...

Radek: Dany jest ciąg arytmetyczny (an ) , gdzie n ≥ 1 . Wiadomo, że dla każdego n ≥ 1 suma n początkowych wyrazów Sn = a ₁ + a₂ + ⋅⋅⋅ + an wyraża się wzorem: Sn = −n² + 13n . Wyznacz wzór na n –ty wyraz ciągu a_n .

pigor: ..., bo S₁ czytasz tak : suma pierwszego (jednego) wyrazu, a więc S₁=a₁, analogicznie S₂=a₁+a₂ − suma dwóch pierwszych, itp. S_n+1= a₁+a₂+...+a_n−1+a_n= S_n+a_n+1= S_n−1+a_n+a_n+1 ...

Radek: mietek a Ty chyba nigdy tego rozumu nie miałeś...i chyba szybko mieć nie będziesz...

mietek: zadania z podstawówki...

Mila: S₁=a₁ suma jednego wyrazu Z drugiej strony masz podane, że sumę obliczamy: S_n=n²+5n zatem S₁=1²+5*1=1+5=6 itd S₂=a₁+a₂ ogólny wzór a_n=S_n−S_n−1

mietek: tyle co mam mnie wystarcza... za to jak widzę o co ty czasem pytasz, to ręce opadają...

Radek: mietek znowu zaczynasz ? Nie rozwiązałeś żadnego zadania a tylko się wymądrzasz, wyłącz internet bo szkodzi na reszte Twoich szarych komórek a chyba wiele juz ich nie zostało Dobrze, wyznaczę a_n z tego

Radek: W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu?

mietek: a₁+...a_2n+1=44 a₂+a_2n=33 n=3, wszystkich wyrazów 7 i nie twierdź, że nie umiem tak prostych zadań ...

Radek: skopiowałeś z internetu...

mietek: a ty tracisz czas na wskazówki, których i tak nie umiesz wykorzystać...

Radek: Powiedziałeś co wiedziałeś to teraz wyjdź...

misiu: https://matematykaszkolna.pl/forum/181502.html

Mila: Nie włączam się w awanturki młodzieży, jak będzie spokój i potrzeba pomocy, to Radek zgłoś.

bezendu: https://matematykaszkolna.pl/forum/237752.html Mila zobacz to jest typ z pod ciemnej gwiazdy.. Tylko co on na forum robi ?

Radek: Pani Milu może Pani wytłumaczyć to zadanie ostatnie ?

bezendu: Tylko spamujesz a śmieszny nie jesteś... Jak długo nad tym myślałeś ? Ale kończę już

Radek: ?

Mila: Ogladałeś rozwiązania Ety podane w linku?

Radek: Tam jeszcze więcej zmiennych mam..

Eta:

mietek : mój sposób był ok...

Eta: @mietka .... jeszcze raz się "wetniesz" z niestosownym komentarzem to Cię zablokuję !

bezendu: Już dawno to trzeba było zrobić...

Mila: To może z sum. Masz 2n+1 wszystkich wyrazów ciągu n jest wyrazów o parzystych numerach (n+1) jest wyrazów o nieparzystych numerach. sumuję wyrazy o nieparzystch indeksach:

	a1+a2n+1
44=		*(n+1)⇔
	2

	a1+a1+(2n+1−1)*r		2a1+2n*r
44=		*(n+1)⇔44=		*(n+1)
	2		2

sumuję wyrazy o parzystch indeksach:

	a2+a2n		a1+r+a1+(2n−1)*r
33=		*n⇔33=		*n⇔
	2		2

	2a1+2n*r
33=		*n
	2

	2a1+2n*r
44=		*(n+1) teraz analizuj, potem podziel stronami i obliczysz n.
	2

Radek: Tylko czemu n+1 ?

Mila: Mietek, pomysł dobry, ale problem polega na wytłumaczeniu. I pamietaj nikogo nie należy obrażać. W danym momencie ktoś nie umie, ale nauczy się. Po niegrzecznym komentarzu pozostaje uraza. To zadanie można rozwiązać na wiele sposobów.

Radek: Pani Milu mietek przekopiował z internetu... skąd to n+1 ?

Mila: Wszystkich wyrazów jest (2n+1, np. 25) 2n:2=n połowa wyrazów bez ostatniego n+1=n+1

Radek: już prawie rozumiem

Mila: No to szoruj dalej, abym widziała, że rozumiesz.

Radek: Ale to tylko jedno równania było potrzebne do wyznaczenia n ?

Mila: Nie rozumiem Cię Radku. Wyznaczyłeś n?

Radek: a₁n+n²r=33 n(a₁+n)=33

Mila: 22: 00 dzielę stronami równania:

33		n
	=		teraz licz n , bo w Twoich równaniach są 3 niewiadome.
44		n+1

Radek:

	33
Skąd ten stosunek		?
	44

walt: Patrz na komentarz Mili z godziny 22:00

Mila: No i ?

Radek: Ja mam dwa równania czy to jest układ równań ?

walt: Masz dwa równania.. teraz możesz je podzielić stronami.. .. ostatecznie Mila już Ci to obliczyła bo wstawiła:

33		n
	=
44		n+1

Radek: Czyli muszę je przyrównać najpierw ?

walt: hm, może zostańmy przy tym, że masz podzielić te wyrazy stronami. Czyli: dzielisz pierwsze równanie przez drugie

	33
po lewej stronie masz
	44

po stronie prawej skraca się w jednym jak i drugim równaniu wyrażenie:

2a1+2n*r
2

	n
dzięki czemu zostaje jedynie:
	n+1

ostatecznie:

33		n
	=
44		n+1

mam nadzieję, że pomogłem

Mila: Radek w obu równaniach masz jednakowe wyrażenie

2a1+2n*r
	=(a1+n*r) mozesz je oznaczyć x
2

wtedy masz : x=(a₁+n*r) podstawiam do równań 33=x*n 44=x*(n+1) rozwiązuj ten układ. ( ja podzieliłam)górę przez dółi pozbyłam się w ten sposób x−a)

Radek: Dobrze, ale i tak wrócę do tego zadania jutro bo jest trudne jak dla mnie.

Radek: Dziękuję Pani Milu ale nadal nie wiem czemu mamy to przyrównać ?

Mila: Chcemy obliczyć n

	33
Z pierwszego :x=
	n

	44
Z drugiego: x=
	n+1

⇔

33		44
	=
n		n+1

oblicz z tego n

Radek: 33(n+1)=44n 33n+33=44n −11n=−33 n=3

Mila: No i dobrze , oblicz ile wyrazów ma ten ciąg ( na początku pisałam).

Radek: 2n+1=7

Mila: To który wyraz jest w środku ( jaki ma numer?) I co jeszcze chcieli?

Radek: 4 jest środkowy.i to wszystko do tego zadania.

Mila: a₄ to środkowy wyraz tego ciągu, jeszcze trzeba podać jaką ma wartość.

Radek: ze wzoru na sumę tak ?

Mila: Tak. ale znowu będą 2 niewiadome. Zrobimy inaczej. Popatrz: 2 4 6 8 10 masz 5 wyrazów c. arytm. , środkowy wyraz to 6. 6*5=30 i 2+4+6+8+10=30 W Twoim zadaniu: 33+44=77 suma wszystkich 7 wyrazów. a₄*7=77 a₄=11 To jest zasada dla c. arytm. o nieparzystej liczbie wyrazów : Suma= środkowy wyraz ( inaczej mediana) * Liczba wyrazów Może sam dojdziesz dlaczego tak jest, albo jutro Ci wyjaśnie.

Radek: Pomyślę nad tym i dam jutro odp. Dziękuję za cierpliwość do mnie bo to anielska cierpliwość. Dobranoc.

Mila: Dobranoc

mietek: i tak tego nie zrozumiesz...