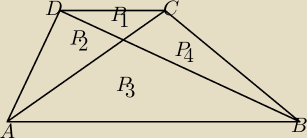
podobieństwo Paga: Przekątne trapezu podzieliły go na cztery trójkąty. Niech P1, P2, P3 i P4 oznaczają pola tych trójkątów. Oblicz pole trapezu, gdy: P1=14, P2=35 Trzeba z podobieństwa tylko nie widzę tych podobieństw.... ΔABD~ΔABC a ΔACD~ΔDBC I co dalej? Patrzyłam tutaj: https://matematykaszkolna.pl/forum/110203.html ale wciąż nie rozumiem.

jakubs: Zauważ, że P2=P4. P4=P2=√P1*P3 35=√14*P3

	175
P3=
	2

Teraz wzór na pole trapezu P=(√P1+√P3)²

pigor: ..., otóż, łatwo wykazać, że p₂=p₄ , więc P _t = 2p₂+p₁+p₃=2*35+14+p₃= 84+p₃= ? , ale

	p3		p4		p4
np.		=		⇒ p3= p2*		=
	P2		p1		p1

	35
= 35*		= 52*35= 87,5, zatem P t = 84+87,5 = 171,5 .
	14

Paga: Skąd wzór na P2=√P1*P3 ?

Paga: a no i jeszcze skąd wiemy że P₂=P₄ ? jak to zapisać?

jakubs: W podanym linku wszystko masz wytlumaczone P=P1+2P4+P3 . Zauważ wzór skróconego mnożenia P=(√P1+√P3)² Jak rozłożysz wzór skróconego mnożenia to otrzymasz 2√P1*√P3=2P4. Dalej otrzymujesz P4=√P1*P3 . P2+P3=P3+P4 P2=P4

Paga: ok. "już" widzę i chyba...rozumiem dziękuję.