DOMELKI DLA MATURZYSTÓW − 4 − DOWODY Domel: DOMELKI DLA MATURZYSTÓW − 4 − DOWODY Udowodnij, że 10ⁿ − 4 jest podzielne przez 6

wredulus_pospolitus: łeee ... a czemu ja nie mogę

Hajtowy: 10ⁿ−4 = 10ⁿ−1−3 = 9(1+10+...+10ⁿ⁻¹)−3

Domel: No Hajtowy i co z tego mamy? Ani 9 ani 3 nie dzielą się bez reszty przez 6

Hajtowy: Ale dzieli się przez 2 i 3

Hajtowy: No ale dobra, już się nie odzywam... niech się Rozszerzeni wypowiedzą

Domel: Cześć wredulus − daj się wykazać nieprofesjonalistom bo ciebie to podejrzewam, że byś mi czasem rozwiązał problem indukcją matematyczną

Domel: Hajtowy − każdy człon sumy musi być podzielny przez 2 i 3

ICSP: 10ⁿ − 4 = 10ⁿ − 10 + 6 = 10(10ⁿ⁻¹ − 1) + 6 Wystarczy pokazać, że 10(10ⁿ⁻¹ −1) jest podzielne przez 6. Zauważamy: 10 ≡ 1 mod 9 10ⁿ⁻¹ − 1 ≡ 0 mod 9 zatem 10ⁿ⁻¹ −1 jest podzielne przez 9. Stąd 10(10ⁿ⁻¹ −1) jest podzielne przez 6.

Domel: O kurde − prawie akademicki wywód a może ktoś prościej spróbuje?

ICSP: analogicznie jak mój, tylko sposobami bardziej licealnymi 10ⁿ⁻¹ − 1 będzie się składało z samych 9, stąd mamy podzielność przez 9. Iloczyn liczb podzielnych przez 2 i przez 3 jest liczbą podzielną przez 6.

Domel: Ale laik może nie zauważyć samych 9 to może rozłożyć 10(10ⁿ⁻¹ − 1) = 10(10 − 1)(10ⁿ⁻² + 10ⁿ⁻³ + ... + 10² + 10 + 1) 10(10ⁿ⁻¹ − 1) = 10*9*(10ⁿ⁻² + 10ⁿ⁻³ + ... + 10² + 10 + 1) no i tu wyraźnie widać że jest i 2 i 3

domel: Zad. 2 Udowodnić, że trapez o podstawach AB i CD ( |AB| > |CD| ) można podzielić prostą równoległą do któregokolwiek boku nie będącego podstawą na dwa czworokąty o równych polach wtedy i tylko wtedy gdy |AB| < 3|CD|

Domel: No i który ma cojones i to rozwali? (no wredulusi i inni zawodowcy − tylko wskazówki )

Godzio: A może tak: 10ⁿ − 4, n ≥ 1 10ⁿ − 4 jest podzielne przez 6 bo: − dzieli się przez dwa (różnica dwóch liczb parzystych jest parzysta) − dzieli się przez trzy, popatrzmy na tą liczbę: 10ⁿ − 4 = 999...9996 −−− każda z cyfr dzieli się przez 3, wiec i suma co kończy dowód

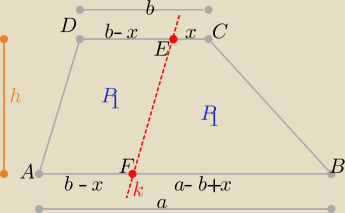
Eta: k∥AD b>a i 0<x<b i b+x<a ⇒ x<a−b z równości pól równoległoboku ADEF i trapezu EFBC

	2x+a−b		3b−a
(b−x)=		⇒ 2b−2x=2x+a−b ⇒ x=		to a<3b bo x>0
	2		4

to |AB|<3|DC|

Domel: Wazyl zrobił to też na stronie https://matematykaszkolna.pl/forum/240153.html

Eta:

Paga: Domel a mogę to zapisać tak? 10ⁿ−4= 2(5ⁿ−2) 5ⁿ ma zawsze na końcu 5 jeśli odejmę 2 będzie 3, a 3*2=6 ?

ICSP: 2 * 5ⁿ ≠ 10 ⁿ

Domel: Zad. 3.

	n3		n2		n
Udowodnić, że suma		+		+		jest liczbą naturalną dla każdej liczby
	6		2		3

naturalnej n

Saizou : hahah robiłem to zadanie w tym tygodniu

Domel: Zad. 4. Udowodnij, że suma 5ⁿ + 2*3ⁿ⁻¹ + 1 jest podzielna przez 8

pawel95:

n3		n2		n		n3 + 3n + 2		n(n2 + 3n + 2)
	+		+		=		=		=
6		2		3		6		6

	n(n+1)(n+2)
	6

n(n+1)(n+2) jako iloczyn 3 kolejnych licz naturalnych dzieli sie przez 2 i przez 3 ,wiec dzieli sie przez tez przez 6.

Domel:

pawel95: 5ⁿ + 2*3ⁿ⁻¹ + 1 dla n =0 1 + 2/3 + 1 nd. dla n = 1 5+0+1=6 nd dla n=2 25 + 2*3 + 1 = 32 dla n=3 125 + 2*9 + 1 = 144 hipoteza 5ⁿ + 2*3ⁿ⁻¹ + 1 dzieli sie przez 8 dla n ≥ 2 zakaldam ,ze dla n = k sie dzieli ( dla n = 2 juz wykazane ) dla n = k+1 5*5ⁿ + 3*2*3ⁿ⁻¹ + 1 = ( 5ⁿ + 2*3ⁿ⁻¹ + 1 ) + 4*5ⁿ + 4*3ⁿ⁻¹ dzieli sie z zal. = 4(5ⁿ + 3ⁿ⁻¹) dzieli sie przez 5 i jako suma 2 liczb nieparzystych przez 2, wiec dzileli sie przez 8

pawel95: w ostatnim " dzieli sie przez 4 i jako ... " jak nie mozna z indukcji,bo nie bylo tak w zadaniu to pozniej sie pomecze jeszcze

Domel: nooo dla n = 1 też się dzieli przez 8 bo 3ⁿ⁻¹ = 1

Domel: Ale indukcji podobno nie ma w programie szkół maturalnych − to poszukajmy innych dróg

pawel95: haha :! no raczej

Saizou : też chciałem zrobić to z indukcji ale Domel nie powiedział że to dla liczb naturalnych

pawel95: tak czy siak trzeba znalezc inne rozwiazanie, ale ja sie poddaje. przynajmniej na dzisiaj "/ zycze powodzenia =]

Domel: No n∊N

Domel: No i jak tam brać maturalna Nie wierzę, że was wystraszyło zad. 4

Domel: Może pomoże zależność a^x − 1 = (a − 1)(a^x−1 + a^x−2 + a^x−3 + ... + a² + a + 1) No a co to jest a^x−1 + a^x−2 + a^x−3 + ... + a² + a + 1 ?

Saizou : Domel ale chyba w ten sposób to gra w kółko

Maslanek: Niekoniecznie 5ⁿ=5*5ⁿ⁻¹ Wtedy 5ⁿ⁻¹−1=(5−1)(5ⁿ⁻²+...+1)=4*(5ⁿ⁻²+...+1) Czyli 5ⁿ=20*(5ⁿ⁻²+...+1) 2*(3ⁿ⁻¹−1)=4*(3ⁿ⁻²+...+1) Z tego wszystkiego mamy: 20*(5ⁿ⁻²+...+1)+5 + 4*(3ⁿ⁻²+...+1)+2 + 1 20*(5ⁿ⁻²+...+1)+4*(3ⁿ⁻²+...+1)+8 4*(5*(5ⁿ⁻²+...+1)+(3ⁿ⁻²+...+1)) + 8 Trzeba by pokazać jeszcze, że 5*(5ⁿ⁻²+...+1)+(3ⁿ⁻²+...+1) jest podzielne przez 2.

Maslanek: Można by uzasadnić ustnie. Jeżeli (n−2) jest nieparzyste, to mamy (n−1), czyli parzystą liczbę składników. Suma parzystej liczby nieparzystych składników jest parzysta. Wtedy teza jest już oczywista. Jeżeli (n−2) jest parzyste, to mamy (n−1), czyli nieparzystą liczbę składników. Czyli suma jest nieparzysta. Ale całość jest sumą dwóch składników nieparzystych, więc całość jest parzysta.