DOMELKI DLA MATURZYSTÓW - 1 - CIĄGI
Domel: DOMELKI DLA MATURZYSTÓW − 1 − CIĄGI
Niech {xn} będzie ciągiem liczbowym spełniającym warunki:
log2 x1 = −2 oraz log2 xn − log2 xn−1 = −2 dla n ≥ 2.
Obliczyć granicę wyrażenia x1 + x2 + x3 + .... + xn przy n→+oo
4 mar 17:21
Paulina:
Dla maturzystów ? Granice ciągu nie obowiązują na maturze 2014.
4 mar 17:22
Saizou :
log
2x
1=−2
log
2x
n−log
2x
n−1=−2
| | 1 | | 1 | |
xn to ciąg geometryczny o x1= |
| i q= |
| |
| | 4 | | 4 | |
zatem
| | 1 | |
a przy n−>+∞ otrzymamy |
| |
| | 3 | |
4 mar 17:27
Domel: Saizou 
A faktycznie − granice chyba wypadły
4 mar 17:31
Saizou : ale ta granica była wyjątkowo łatwa
4 mar 17:41
Domel: Zad. 2
Wyznaczyć wszystkie wartości x, dla których liczby 2, (2x + 3) i (2x + 27) są odpowiednio
pierwszym, trzecim i piątym wyrazem ciągu geometrycznego
5 mar 11:51
Ajtek:
Miłe zadanko
.
5 mar 12:03
Domel: Zadanko wapniaków robiących matury w latach 80−tych
5 mar 14:04
Ajtek:
Nikt się nie wziął
Przecież rozwiązanie zajmuje 3 minuty
5 mar 16:06
Domel: Chyba się wystraszyli x−ów w potędze
5 mar 17:44
Wazyl: 2x+1+54=22x+12*2x+9
2x=t i dalej!
5 mar 17:57
ciemnota: 2
x=t
(t+3)
2=(t+27)2
t
2+6t+9=2t+54
t
2+4t−45=0
delta=16−4*1*(−45)=16+180=196
√d=14
t
1=−9 t
2=7
2
x=−9 i 2
x=7
No i jak mam to zamienić
5 mar 19:45
Piotr 10: jeśli to jest dobrze to
2x= − 0
x∊∅ a
2x=7
log27=x
5 mar 19:46
ciemnota: Łe to pewnie źle zrobiłem.
5 mar 19:49
domel: Piotr 10 coś namieszałeś
ax = b => loga b = x
5 mar 19:51
domel: ciemnota − na razie masz very good
ciągnij to dalej wg mojej podpowiedzi
5 mar 19:53
Piotr 10: logac=b ⇔ ab=c.
5 mar 19:55
ZKS:
x = log25
5 mar 19:56
domel: tylko pamiętaj
log
a b = x to „b” musi być jakie
?
5 mar 19:56
ZKS:
Policz jeszcze raz t2.
5 mar 19:57
domel: ciemnota − tylko, że t2 jest 5 a nie 7
5 mar 19:59
Antek: Ja jestem akuratnie ten wapniak ktory pisal mature w 1984r
5 mar 20:00
ciemnota: 2x=−9 no to co mogę z tego zrobić chyba nic jest ujemna
2x=5
log25=x
Nie poddaje się dalej już nie wiem.
5 mar 20:04
abc:
domel zapomniał? ,że też niedłuo będzie
wapniakiem ?
5 mar 20:06
abc:
Póki co jest
cwaniakiem 
5 mar 20:06
Antek: Chociaz teraz nazywaja nas juz sarkofagi
5 mar 20:25
Domel: ciemnota − rozwiązałeś
A od wapniaków
to się możecie jeszcze co nieco nauczyć
5 mar 20:55
Wazyl: Domel może jeszcze jakiś mały "ciągnik"?
Ode mnie dla rówieśników też mam:
Oblicz sumę:
| | 1 | | 2 | | 3 | | n | |
Sn= |
| + |
| + |
| +....+ |
| |
| | 2! | | 3! | | 4! | | (n+1)! | |
5 mar 21:00
Ajtek:
Ruszyli zadanko
5 mar 21:04
5 mar 21:08
Wazyl:
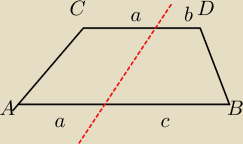
zacząłbym tak :
2a=c+b
3a−c=a+b
Musimy wykazać 3(a+b)<a+c
Tutaj stanąłem. Zaraz wykombinuję.
5 mar 21:20
Wazyl: 3a+3b=a+c+4b
3(a+b)>a+c
cnw.
5 mar 21:23
Wazyl: 21:20 powinno być > a nie <. Teraz tak spojrzałem.
5 mar 21:34
Domel:
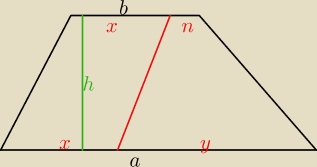
Ja wprawdzie poszedłem troszkę inną drogą − ale wynik masz prawidłowy:
1. Żeby były dwa czworokąty to n > 0
| | 1 | | a + b | |
2. Ponieważ te czworokąty są połową trapezu to: xh = |
| ( |
| h) |
| | 2 | | 2 | |
| | a + b | | 4b − a − b | |
n = b − x = b − |
| = |
| |
| | 4 | | 4 | |
3b − a > 0 => 3b > a
5 mar 21:52
5 mar 21:54
Paulina:
Eta od kiedy Ty maturzystka ?
5 mar 21:55
Eta:
1LO ... no to za 2lata
5 mar 21:56
Saizou :
5 mar 21:57
Eta:
5 mar 21:58
Paulina:
Nie ładnie kłamać ? Skoro spotkałam Twoje posty z ponad 4 lat
5 mar 21:58
Eta:
No bo wtedy byłam w podstawówce
5 mar 21:58
Saizou : a czy to w czymś przeszkadza ?
5 mar 21:59
Paulina:
Nie wierzę, a po drugie pisałaś o rozwiązywaniu zadań na emeryturze więc jesteś Panią od matmy
5 mar 22:00
Eta:
5 mar 22:01
Saizou : jaką panią, po prostu naszą
Etą od
5 mar 22:03
Domel: Oj − tylko bez awantur drogie Panie (i Panowie)
5 mar 22:04
Paulina:
Nikt nie robi awantur ale poziom matematyki jaki reprezentuje Eta jest o wiele wyższy niż
ucznia lo !
5 mar 22:06
Eta:
5 mar 22:07
Maslanek: A jabłka czerwone jakby sadownikiem była od conajmniej 40 lat
5 mar 22:08
Wazyl: a co z moim zadaniem? Nikt nie chce zrobić?
5 mar 22:18
Domel: No bo I LO = I Liga Ogólnopolska (no chyba nie Ogólnoświatowa)
5 mar 22:19
Paulina:
Nie chcemy Ci odbierać tej przyjemności.
5 mar 22:19
Domel: Wazyl − poczekaj − jeszcze się ruszą
A swoją drogą, że to
Eta wykazała się, że ma cojones to hmmmm − na szczęście
Wazyl
uratowałeś nasz honor
5 mar 22:23
Wazyl: Ja już je zrobiłem
Pora na Ciebie
5 mar 22:23
Wazyl: Domel Ty szkolniak czy "wapniak"?
5 mar 22:24
Saizou : Domel ja nie potrafię po hiszpańsku
5 mar 22:24
Paulina: Ja mam swoje funkcje i robię zadania z funkcji. Nie chcę dodatkowych zadań bo mam ich dosyć
10 matematyk w tygodniu
5 mar 22:25
Domel: Noooooo cóż − matmę ostatni raz miałem 24 lata temu (no może 23) a teraz mam pewnego osobnika,
który próbuje przygotować się do matury. No to muszę sobie co nieco odświeżyć
5 mar 22:53
Domel: Dlatego też czasami walę jak łysy kucykiem − więc jak czasem się pomylę to please o
wyrozumiałość − wiecie synapsy się już sypią, zęby się kruszą, wzrok mętnieje
5 mar 22:55
Saizou : oj tam oj tam, wzrok mi też już mętnieje od 5 lat
5 mar 22:56
Domel: Saizou nie oglądałeś Desperado z Antonio Banderasem? No cóż cojones to są noooo − zajrzys
do słownika polsko−hiszpańskiego
5 mar 22:58
Saizou : na tyle ten język zdołałem poznać, ale polskie określenie mi się bardziej podoba
5 mar 22:59
5 mar 23:04
zombi: Tak
5 mar 23:07
Ajtek:
Paulina zdziwiłabyś się, poznając
Vax'a .
Witam obecnych
.
5 mar 23:20
zombi: Cześć
5 mar 23:22
Domel: No oki −
Wazyl i
Saizou pewnie już tulą poduszkę
Próbuję dojść jaka to będzie suma w zadaniu
Wazyla
| | 1 | | n | |
Wychodzi mi a1 = |
| a iloraz q = |
| |
| | 2! | | n2 − 1 | |
No i jak tu dojść do sumy ciągu?
Jakaś wskazówka?
6 mar 00:55
Domel: Hmmm − oblicz sumę:
| | 1 | | 2 | | 3 | | n | |
Sn = |
| + |
| + |
| + ... + |
| |
| | 2! | | 3! | | 4! | | (n + 1)! | |
6 mar 01:05
Domel: Czy wychodzę z tego?
| | k | | k | |
Sn = ∑nk=1 |
| = ∑nk=1 |
| |
| | (k + 1)! | | (k −1)!*k*(k+1) | |
| | 1 | |
Sn = ∑nk=1 |
| |
| | (k −1)!*(k+1) | |
i co dalej
6 mar 03:03
Wazyl: Saizu
6 mar 14:20
Wazyl: Domel pokombinuj inaczej w tym mianowniku.!
6 mar 14:22
Wazyl: Saizu jak poradziłeś sobie z tym to trzymaj następne:
Oblicz sumę: 1*1!+2*2!+3*3!+...+n*n!
6 mar 14:34
Domel: Czy o taki mianownik by szło?
Następne elementy jakieś dziwne
6 mar 14:46
Wazyl: Po co to "k" do mianownika wywaliłeś?
6 mar 15:07
Domel: No normalnie to jest:
Jak to dalej rozwinąć?
6 mar 15:12
Domel: a to k w mianowniku
? − patrzyłem czy licznik w postaci "1" mi czegoś nie da
6 mar 15:18
6 mar 15:19
Domel: No i ooooooooooo
| | 1 | | 1 | |
Sn = ∑nk=1 ( |
| − |
| ) |
| | k! | | (k+1)! | |
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
Sn = (1− |
| )+( |
| − |
| )+( |
| − |
| )+...+( |
| − |
| ) |
| | 2! | | 2! | | 3! | | 3! | | 4! | | n! | | (n +1)! | |
6 mar 15:49
Wazyl:
6 mar 15:52
Domel: No i idąc tym tropem mam sumę twojego następnego zadania − masz dar popychania
6 mar 16:01
Domel: Podam tylko wynik do kontroli a metodologię zostawię chętnym
1*1! + 2*2! + 3*3! + ... + n*n!
Sn = (n + 1)! − 1
6 mar 16:03
Saizou :
Wazyl tylko jest jeden problem z tym zadaniem
ja jeszcze nigdy nie spotkałem się aby na
maturze był znak sumy i ciąg z silniami
6 mar 16:57
Domel: Ale ja wierzę w ciebie
Saizou
6 mar 17:18
Saizou : tak tylko informuję, zawsze lepiej wiedzieć więcej niż za mało xd
6 mar 17:20
Wazyl: domel!
6 mar 17:43
Domel: Zad. 3
| | n−1 | |
Suma n ≥ 2 początkowych wyrazów ciągu (an) opisana jest wzorem Sn = |
| . |
| | n | |
Podaj wzór na wyraz a
n dla n ≥ 2 tego ciągu.
6 mar 19:41
Saizou :
a
n=S
n−S
n−1
| | n−1 | | n−2 | | n2−2n+1−n2+2n | | 1 | |
an= |
| − |
| = |
| = |
| |
| | n | | n−1 | | n(n−1) | | n(n−1) | |
6 mar 19:46
Domel: Zad. 4
Oblicz sumę szeregu:
| | 1 | | 1 | | 1 | | 1 | | 1 | |
Sn = |
| + |
| + |
| + |
| + ... + |
| |
| | 2 | | 6 | | 12 | | 20 | | n(n+1) | |
Wazyl daj szansę innym
6 mar 20:05
Saizou :
Domel szeregów też nie ma
6 mar 20:10
Domel: No dobra − to jest pewien ciąg − w drugą stronę policzyłeś poprzednie zadanie (czyli n−ty wyraz
szeregu/ciągu)
A liczenie sumy ciągu niearytmetycznego i niegeometrycznego macie?
6 mar 20:26
Saizou : powiem ci w tajemnicy poliszynela że nie, program jest strasznie okrojony
6 mar 20:36
6 mar 20:46
zombi: Domel S=1?
6 mar 20:56
Saizou : hahah ja ambitny? po prostu czasami coś mi wyjdzie xd
6 mar 21:01
Domel: No granica przy n→oo to jest 1 ale mi chodzi o ogólny wzór na sumę n−wyrazów
Wazyl może będziesz musiał wesprzeć kolegów − chociaż podpowiedzią może być twój
post z 15:19
6 mar 21:31
zombi: | | 1 | |
Sn = 1 − |
| to miałeś na myśli? |
| | n+1 | |
6 mar 21:36
Wazyl:
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
Sn=( |
| − |
| )+( |
| − |
| )+....+( |
| − |
| )=1− |
| |
| | 1 | | 2 | | 2 | | 2 | | n | | n+1 | | n+1 | |
6 mar 21:43
Domel: | | 1 | | 1 | |
No w drugim członie powinno być +( |
| − |
| ) − ale wynik |
| | 2 | | 3 | |
6 mar 21:55
Wazyl: Ehhh litrówka!
6 mar 22:00
zombi: No to dobrze napisałem...
6 mar 22:19
Domel: Zad. 4
Obliczyć trzeci wyraz ciągu 2x1, 2x2, 2x3, ....., 2xn wiedząc, że jest
to ciąg geometryczny i że x1 + x2 + ... + x10 = 110 oraz x7 = 14
7 mar 10:58
J:
(2
x2)
2 = (2
x1)(2
x3) ⇔ 2x
2 = x
1 + x
3 ,
czyli ciąg x
1,x
2,x
3 .... x
n jest arytmetyczny.
x
1 = 14 − 6r
x
10 = 14 + 3 r
| | 14 −6r + 14 +3r | |
110 = |
| *10 ⇔ 22 = 28 − 3r ⇔ r = 2 |
| | 2 | |
x
1 = 14 − 12 = 2
x
2 = 2 +2 = 4
x
3 = 4 +2 = 6
Zatem trzeci wyraz ciagu: 2
x3 = 2
6
7 mar 12:29
Domel:
I gdzież to po maturze? Warszawa?, Gdańsk? Wrocław? A może stolica Warmii i Mazur − Olsztyn?
7 mar 12:50
J: Już prawie nie pamietam,kiedy ją zdawałem
, ale w Krakowie.
7 mar 12:53
Domel: Eeeeee feeeee
− daj szansę maturzystom
7 mar 13:02
J: Poprawię się
7 mar 13:04
Domel: Zad. 5
Podaj ogólny wyraz a
n ciągu:
No
Wazyl jak dla tego ciągu wyprowadzisz wzór na sumę toooo − berecik z głowy i szacuun
7 mar 13:23
7 mar 13:41
zawodus: Na pewno nie
7 mar 15:31
7 mar 15:33
Domel:
| | 1 | | 1 | |
chyba nie − zobacz, że dla n = 1 z twojego wzoru wychodzi S1 = − |
| a nie + |
| no |
| | 2 | | 2 | |
i wg twojego wzoru nie istnieje wynik dla n = 2 (wyjdzie 0 w mianowniku)
7 mar 15:34
J: Nie tylko w mianowniku
7 mar 15:36
Domel: No a jaki jest ogólny wyraz ciągu a
n? Suma szeregu to wisienka na torcie
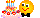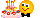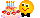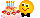
7 mar 15:41
7 mar 17:51
zawodus: To ja was załatwię
7 mar 18:13
Domel:
7 mar 18:19
Wazyl:
7 mar 19:05
