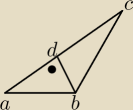
Planimetria Maturzystka: Proszę o pomoc W trójkącie rozwartokątnym ABC poprowadzono wysokość BD, która podzieliła ten trójkąt na dwa trójkąty tak,że trójkąt ADB jest równoramienny. Oblicz długość promienia R okręgu opisanego na trójkącie ABC. |AB|=4 √2 |BC|=4(1+ √3) Wiem że trzeba zastosować twierdzenie sinusów tylko mam problem z obliczeniem kątów przy wierzchołkach, złe wyniki mi wychodzą.

Bizon: ... to zadanko można i w gimnazjum Znasz |AB| ... wiesz, że |AD|=|BD| ....znasz kąt przy wierzchołku A i przy B ...znasz więc i |AD| i |BD| Znasz |BC| ...znasz więc i |CD| ... znasz wszystko −

Maturzystka: |CD| licze z pitagorasa ΔBCD i |CD|²=32 √3 + 48 gdyby CD wyszło mogłabym obliczyć tangens kąta alfa przy wierzchołku c i później z górki... tylko mam problem z odcinkiem CD

Bizon: ... ciekawy ten Twój Pitagoras −

Bizon: ... to może powiedz jaka jest miara długości |AD| l |BD|

Maturzystka: 4 cm i 4 cm

Bizon: to teraz licz to |CD|

Kamix: Bizon mógłbyś pomóc, bardzo proszę https://matematykaszkolna.pl/forum/240146.html

Maturzystka: 4²+|CD|²=[4(1+ √3)]²

Maturzystka: Wiem że to jest banalne zadanie i coś musze mieszać, że mi nie chce wyjść

kamila: .

maturzystka: Prosze chcialabym juz skonczyc to zadanie.

maturzystka: .