zadanie maturalne anka: W układzie współrzędnych na płaszczyźnie zaznaczono punkty A(5;1) i B(9;3), Wyznacz wszystkie możliwe położenia punktu C, dla których ABC jest trójkątem równoramiennym o podstawie AB i polu równym 10.

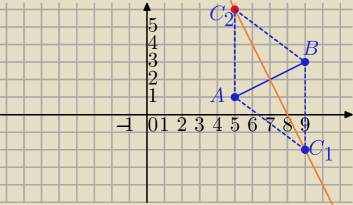
Mila: A(5;1) i B(9;3) Punkt C leży na symetralnej odcinka AB. Symetralna AB to zbiór wszystkich punktów jednakowo odległych od punktów A i B. P(x,y) − dowolny punkt symetralnej AB. √(x−5)²+(y−1)²=√(x−9)²+(y−3)² /² (x−5)²+(y−1)²=(x−9)²+(y−3)² x²−10x+25+y²−2y+1=x²−18x+81+y²−6y+9 −10x+26−2y=−18x−6y+90 4y=−8x+64 s: y=−2x+16 symetralna AB |AB|=√4²+2²=√20=2√5

	1
PΔABC=10=		*2√5*h⇔
	2

√5*h=10

	10		10√5
h=		=		=2√5
	√5		5

	5+9		1+3
S=(		,		)=(7,2) wsp.środka AB
	2		2

Punkt C będzie punktem przecięcia symetralnej AB i okręgu (x−7)²+(y−2)²=(2√5)² y=−2x+16 rozwiąż ten układ II sposób odległość C od prostej AB jest równa 2√5 Prosta AB: 1=5a+b

	1		3
3=9a+b⇔a=		,b=−
	2		2

	1		3
y=		x−		postać kierunkowa równania prostej AB
	2		2

Symetralna AB: S=(7,2) y=−2x+b i 2=−2*7+b, b=16 s: y=−2x+16 symetralna AB |AB|=√4²+2²=√20=2√5

	1
PΔABC=10=		*2√5*h⇔
	2

√5*h=10

	10		10√5
h=		=		=2√5
	√5		5

x−2y−3=0 postać ogólna równania prostej AB C=(x_c,y_c) i C∊s⇔y_c=−2x_c+16

	|xc−2(−2xc+16)−3|
d=		=2√5
	√1+4

|x_c+4x_c−35|=2√5*√5 |5x_c−35|=10 5x_c−35=10 lu 5x_c−35=−10 x_c=9 lub x_c=5 y_c=−2*9+16=−2 lub y_c=−2*5+16=6 C₁=(9,−2) lub C₂=(5,6)

bezendu: To zadanie chyba z czerwcowej matury 2013. ?

Eta: https://matematykaszkolna.pl/forum/239550.html