planimetria
bezendu:
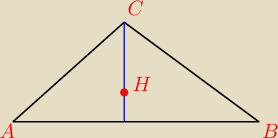
Punkt H jest punktem wspólnym wysokości trójkąta ostrokątnego ABC wpisanego w okrąg o
promieniu 12. Oblicz promień okręgu opisanego na trójkącie ABH .
Można jakąś wskazówkę do zadania ?
27 lut 21:41
zawodus: punktem wspólnym wysokości i czego?
27 lut 21:43
bezendu:
Znowu za mało danych ? Przepisane jest tak jak w książce
27 lut 21:44
52: myślę że środku okręgu
27 lut 21:45
Mila:
CHyba chodzi o punkt przecięcia 3 wysokości tego Δ.?
Narysuj te wysokości, to może coś zauważysz.
27 lut 21:50
bezendu:
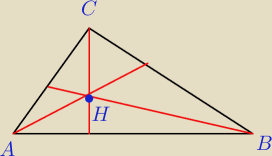
hmm ?
27 lut 21:56
Mila:
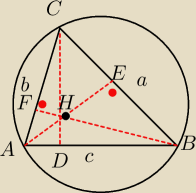
27 lut 21:58
Mila:
Podpowiedź.
∡AHB=∡FHE jako kąty wierzchołkowe, zwiąż to z kątem C i tw sinusów w obu Δ.
27 lut 22:01
bezendu: I nadal nie wiem

27 lut 22:06
Mila:
Druga podpowiedź.
∡C=γ
∡FHE=180−γ z sumy katów w czworokącie FHEC
27 lut 22:10
bezendu:
To z licząc ze wzoru na promień wychodzi R=12
27 lut 22:14
Mila:
Dobrze, jak to liczysz?
27 lut 22:19
27 lut 22:24
27 lut 22:28
bezendu: no tak ze wzorów redukcyjnych, ale napisałem równanie wyjściowe. Zadania niby za 3 punkty a o
wiele trudniejsze od poprzedniego.
27 lut 22:30
Mila:
Robisz mało dokładne szkice.
27 lut 22:46
bezendu:
Na kartce robię dokładne, ale tutaj nie mogę się połapać żeby połączyć te zależności.
27 lut 22:49
bezendu:
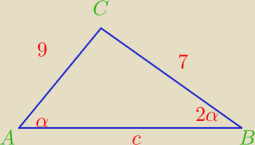
W trójkącie ABC dane są długości boków: |AC | = 9 , |BC | = 7 . Wiadomo też, że miara kąta
∡ABC jest dwa razy większa od miary kąta ∡BAC . Oblicz stosunek długości promienia okręgu
wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
Ale zastanawia mnie czemu nie mogę tego policzyć i jakoś uzależnić
27 lut 23:15
Mila:
Masz cosα to możesz obliczyc c.
27 lut 23:33
Mila:
Potem porównanie pól ze wzorów z r i R.
27 lut 23:34
bezendu:
Ja wiem jak zrobić to zadanie tylko pytam czy można coś zrobić tym sposobem ostania linijka
23:15 ?
27 lut 23:37
Mila:
Pewnie można, ale jak widzę sin(3α) to się zniechęcam i szukam prostszego sposobu.
27 lut 23:45
bezendu:
Dziękuję, muszę jeszcze pomyśleć nad pierwszym pierwszym zadaniem.
27 lut 23:49
bezendu: Może ktoś jeszcze raz wytłumaczyć to pierwsze zadanie ?
28 lut 17:40
Mila:
Czego tam nie rozumiesz?
28 lut 17:49
bezendu:
Czemu trzeba skorzystać z z sumy katów w czworokącie FHEC ?
28 lut 17:54
Mila:
W ten sposób poznasz kąt leżący naprzeciw c=AB w ΔABH i możesz obliczyc z tw. sinusów promień
okręgu opisanego na tym Δ.
28 lut 17:57
bezendu: a co daje informacja o tym promieniu ?
28 lut 18:07
zawodus : To spróbuj rozwiązać bez tej info
28 lut 18:50
bezendu: ?
28 lut 19:55
bezendu: i jeszcze to zadanie 23:15 tez się nie zgadza bo wychodzi
c
2=81+49−81
c
2=49
c=7
i promienie wychodzą inne, a po z tym to nie może być trójkąt równoramienny...
28 lut 20:25
Mila:
Źle zastosowałeś tw. cosinusów. 20:25
72=92+c2−2*9*c*cosα
28 lut 20:30
bezendu:
| | 9 | |
Jak to źle ? Przecież c2=72+92−2*7*9* |
| na to liczyłem ten cos przecież. |
| | 14 | |
28 lut 20:33
zawodus : Źle stosujesz tw cosinusów
28 lut 20:34
Mila:
Zadanie 1)
| c | | c | |
| = |
| =2*R w ΔABC, gdzie R=12 |
| sinC | | sinγ | |
w ΔABH:
| | c | | c | | c | |
2r= |
| = |
| = |
| =2*R⇔r=12 |
| | sin∡AHB | | sin(180−γ | | sinγ | |
28 lut 20:35
Mila:
do 20:33
Przeciwległym kątem do c jest kąt (180−3α).
28 lut 20:36
bezendu: Dziękuję już widzę błąd
28 lut 20:39
bezendu:
Czyli nie mogę użyć mojego pomysłu bo nie znam α i trzeba 20:30 ?
28 lut 20:54
Mila:
Potrzebny byłby cos (3α), mozna to obliczyc, ale to zbędna komplikacja.
28 lut 21:06
bezendu:
Istnieje jakiś wzór na obliczenie długości środkowej ?
28 lut 21:40
Mila:
Istnieje, ale ja nie pamiętam i za każdym razem liczę, a sposób w zależności od danych.
Daj zadanie.
28 lut 21:49
bezendu:
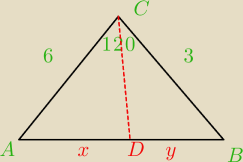
W trójkącie ABC dane są kąt |∡ACB | = 120
0 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta ∡ACB
przecina bok AB w punkcie D .
Oblicz długość odcinka CD .
Wyliczyłem sobie długość boku AB oraz z twierdzenia o dwusiecznej wyliczyłem x oraz y ale jak
policzć AD ? wskazówkę proszę
28 lut 21:57
Saizou :
tw. cosiusów ∡ADC=β
28 lut 22:01
bezendu: ok już liczę
28 lut 22:09
Mila:
Suma pól 2 Δ=pole ΔACB
28 lut 22:15
Saizou : i to jest najprostszy sposób chyba xd
28 lut 22:18
bezendu:
odcinek AB=3
√7
Z twierdzenia o dwusiecznej
6x=9
√7−3x
9x=9
√7
x=
√7
AD=2
√7 AD=p
(2
√7)
2=6
2+p
2−2*p*cos60
28=36+p
2−p
p
2−p+8=0
dela wychodzi ujemna

28 lut 22:21
Mila:
CD=p
Masz pomyłkę.
28=36+p2−6p
28 lut 22:32
Mila:
Zrób z porównaniem pól.
28 lut 22:37
bezendu: Dziękuję teraz juz wychodzi poprawny wynik.
28 lut 22:37
Mila:
II sposobem zrobiłeś?
28 lut 22:43
bezendu:
| 1 | | 1 | |
| *6*p*sin60+ |
| *3*p*sin60=0,5*6*3*sin120 |
| 2 | | 2 | |
9
√3p=18
√3
p=2
28 lut 22:48
Mila: 
28 lut 22:55
bezendu: Jutro będą dowody i okręgi

28 lut 23:05
Mila:
No i pięknie.

Jak w szkole na matematyce?
28 lut 23:19
bezendu:
Cały czas mam sprawdziany powtórzeniowe, tylko dla mnie to nic bo zrobię i dostanę 5 a to tylko
poziom podstawowy więc nie czuję, że w szkole przygotuję się dobrze do matury.
28 lut 23:21
Mila:
No, na pewno nie jest tak źle, jak piszesz.
Poziom podstawowy też jest ważny. Do R przygotowujesz się.
28 lut 23:30
28 lut 23:31
bezendu:
Wracając do zadania 23:15 jak policzyć promień okręgu wpisanego ?
Heronem to paskudnie wychodzi..
1 mar 23:33
bezendu: ?
1 mar 23:41
Mila:
Nie liczysz tych promieni, ale pole Δ w zależności od R i r
i dzielisz
| P(R) | | R | |
| =1 z tego obliczasz |
| albo odwrotnie, co łatwiej, ale są brzydkie liczby. |
| P(r) | | r | |
1 mar 23:45
bezendu:
Dziękuję, bo licząc r wychodził koszmar.
1 mar 23:47
 Punkt H jest punktem wspólnym wysokości trójkąta ostrokątnego ABC wpisanego w okrąg o
promieniu 12. Oblicz promień okręgu opisanego na trójkącie ABH .
Można jakąś wskazówkę do zadania ?
Punkt H jest punktem wspólnym wysokości trójkąta ostrokątnego ABC wpisanego w okrąg o
promieniu 12. Oblicz promień okręgu opisanego na trójkącie ABH .
Można jakąś wskazówkę do zadania ?
 hmm ?
hmm ?


 W trójkącie ABC dane są długości boków: |AC | = 9 , |BC | = 7 . Wiadomo też, że miara kąta
∡ABC jest dwa razy większa od miary kąta ∡BAC . Oblicz stosunek długości promienia okręgu
wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
W trójkącie ABC dane są długości boków: |AC | = 9 , |BC | = 7 . Wiadomo też, że miara kąta
∡ABC jest dwa razy większa od miary kąta ∡BAC . Oblicz stosunek długości promienia okręgu
wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
 W trójkącie ABC dane są kąt |∡ACB | = 1200 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta ∡ACB
przecina bok AB w punkcie D .
Oblicz długość odcinka CD .
Wyliczyłem sobie długość boku AB oraz z twierdzenia o dwusiecznej wyliczyłem x oraz y ale jak
policzć AD ? wskazówkę proszę
W trójkącie ABC dane są kąt |∡ACB | = 1200 , |AC | = 6 i |BC | = 3 . Dwusieczna kąta ∡ACB
przecina bok AB w punkcie D .
Oblicz długość odcinka CD .
Wyliczyłem sobie długość boku AB oraz z twierdzenia o dwusiecznej wyliczyłem x oraz y ale jak
policzć AD ? wskazówkę proszę



 Jak w szkole na matematyce?
Jak w szkole na matematyce?