13
qu: A jak się zabrać za coś takiego ?
Naszkicuj wykres f(x)= log3 (3x+3)
dla jakich argumentów przyjmuje wartości mniejsze od 2 ?
26 lut 23:23
Ajtek:
Narysuj log
3x, krok drugi narysuj log
33x, następnie przesuń ten wykres o ile
w która
stronę
26 lut 23:32
qu: 3 w lewo
26 lut 23:34
Ajtek:
.
26 lut 23:34
Mila:
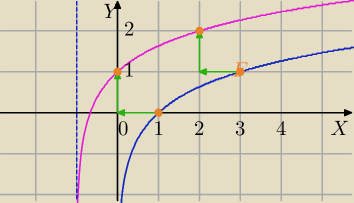
D:x>−1
Ja zrobiłabym tak:
f(x)=log
3(3*(x+1))=log
3(3)+log
3(x+1)
f(x)=1+log
3(x+1)
f1(x)=log3(x)→T
[−1,1]→
f(x)=1+log3(x+1)
26 lut 23:42
Ajtek:
Tak też można
.
26 lut 23:43
pigor: ..., lub
f(x)= log
3 (3x+3)= log
3 3(x+1)= log
33+log
3(x+1)=
1+ log3 (x+1) ,
a więc narysuj wykres (krzywą logarytmiczną)
funkcji
y=log3x i przesuń ją o wektor [−1,1] (w lewo o 1 i o tyle samo do góry),
a więc
x= −1 − asymptota pionowa i
y=1 − pozioma . ...
26 lut 23:43
qu:
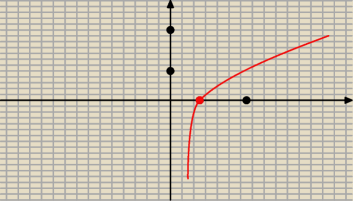
Pierwsza jakoś tak ?
26 lut 23:45
qu: za długo rysowałem..
26 lut 23:46
pigor: ..., o kurcze y=1
to żadna asymptota
rzepraszam idę spać
26 lut 23:48
Ajtek:
Trzymaj się
pigor
26 lut 23:49
qu: chyba z trygonometria Ci się coś pomyliło
26 lut 23:51
Ajtek:
qu jest późno, każdy ma prawo się pomylić. Nawet pomagający
.
26 lut 23:54
qu: żartuję sobie poza tym to cieszę się, że ktoś ma ochotę mi pomóc
26 lut 23:58
Ajtek:
Tym bardziej to szanuj.
26 lut 23:59
qu: mam jeszcze pytanko,
jak szuka się charakterystycznych punktów dla wykresów log
w tym przypadku log3 x
na pewno (1,0) a inne ?
26 lut 23:59
Ajtek:
Szukasz potęg podstawy logarytmu
.
27 lut 00:00
qu: Dziękować
27 lut 00:13
Ajtek:
Prosić
27 lut 00:13
Trivial: Dobranoc Aj.
27 lut 00:14
Ajtek:
Ja jeszcze nie spadam
.
27 lut 00:14
27 lut 00:15
Ajtek:
Trivial, nie chce mi się odrabiać pracy domowej za kogoś
.
A pięknie robi to
Janek191.
27 lut 00:22
qu: w rozwiązaniu Mili x+1 trzeba na wyczucie podstawić, żeby się zgadzało ?
27 lut 00:32
Ajtek:
Nie na wyczucie
Na widzę
27 lut 00:33
qu: dla jakich argumentów przyjmuje wartości mniejsze od 2
dla argumentów < od 2 ?
27 lut 00:43
Ajtek:
dla jakich argumentów
FUNKCJA przyjmuje wartości mniejsze od 2
log
3(3x+3)<2
Odczytasz to pięknie z wykresu
Mili.
Nie gub słów w zadaniu
27 lut 00:48
qu: dla argumentów mniejszych od 2 − zgadza się ?
A gdyby z wykresu nie dało się tak prosto odczytać
to
trzeba to równanie co napisałeś rozwiązać ?
27 lut 00:51
qu: sory nierówność
27 lut 00:52
Ajtek:
Nie masz w poleceniu sposobu rozwiązania. W tym przypadku można rozwiązać to graficznie, jak i
algebraicznie.
Oba sposoby rozwiązywania warto znać
Spokojnej nocy
.
27 lut 00:56
qu: no tak, dzięki
kolorowych snów
27 lut 00:57
Mila:
D: x>−1
log3(3x+3)<2⇔
log3(3x+3)<log3 (9) funkcja rosnąca , bo podstawa logarytmu większa od 1.
3x+3<9 i x∊D
3x<6
x<2 i x>−1
x∊(−1,2) co widać z wykresu godz. 23:42
27 lut 16:52
