Dla jakich wartości parametru m równanie Madzia:

	1
Dla jakich wartości parametru m równanie |		x −3 +2m| +2m= m2−3
	2

a) nie ma rozwiazania b) ma 1 rozwiązanie Dla wyznaczonych wartości m podaj rozwiązania danego równania ************************* Prosiłabym o pomoc. Czy ktoś potrafi rozwiązać to zadanie poprawnie ?

Madzia: .

Madzia: .

Maslanek: Na pewno nie ma rozwiązania dla m²−3<0

	licznik
oraz możliwe, że wtedy kiedy x=		i mianownik=0. Wtedy dla takich m dla
	mianownik

których mianownik się zeruje będzie albo tożsamość, albo sprzeczność. 1 rozwiązanie dla pozostałych m (pomijając to kiedy mianownik się zeruje)

ICSP:

	1
|		− 3 + 2m| = m2 − 2m − 3
	x

Teraz odpowiedz sobie na pytanie. Jaką wartoś musi przyjąć prawa strona aby równanie było sprzeczne, a jaką aby miało jedno rozwiązanie.

Madzia: Maślanek dziękuję bardzo ciekawie to rozpisałeś. ICSP− właśnie tak zrobiłam ale nie pomieszały mi się liczby i nie miałam styczności z takim zadaniem.

Madzia: a mogłabym prosić aby ktoś tak rozpisał to zadanie krok po kroku aby była gotowa odpowiedź ?

Maslanek: Oczywiście Madzia nie zauważyłem, że po lewej jest wolny składnik +2m. Przenosimy na drugą stronę i podobnie jak wyżej opisane przeze mnie Zacznij rozpisywać. Sprawdzimy

Madzia: ok więc zaczynam rozpisywać ale zacznę wpierw od odpowiedzi (tylko mam je w arkuszach ale mi zalezy aby zrozumieć to ! ) a. (−1;3) b. m=−1 ∨ m=3 x=10 , x=−6

Madzia:

	1
|		x −3 +2m| +2m= m2−3
	2

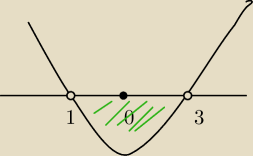
	1
|		x −3 +2m| = m2 −2m −3
	2

Δ<0 Δ= 4−4*1*(−3) Δ=16 √Δ=4 x1= −1 x2=3 a. (−1;3) w sumie to by pasowało do pkt A

Madzia:

	1
|		x −3 +2m| = m2 −2m −3
	2

tutaj Δ=0 i wychodzi punkt B b. m=−1 ∨ m=3

aaagaaa: Przepraszam że się wtrącę, ale bardzo potrzebuje https://matematykaszkolna.pl/forum/238838.html

Madzia: dobra zadanie rozwiązane dzięki chłopaki za to ze mnie naprowadziliście pozdrawiam