dowód Radek: Niech m ,n ∈ R + , udowodnij, że jeżeli m + n = 1 to prawdziwa jest nierówność

	1		1
		+		≥4
	m		n

m+n
	≥4
mn

1
	≥4
mn

1≥4mn /4

1
	≥mn?
4

Mila: dalej tak: m,n∊<0,1> i m+n=1⇔m=1−n Zbadamy jakie wartości przyjmuje funkcja f(n)=n*(1−n) f(n)=n−n² f(n)=−n²+n

	−1		1
nw=		=
	−2		2

	1		1		1		1
f(		)=−		+		=		najwieksza wartość funkcji f(n)⇔
	2		4		2		4

	1
m*n≤
	4

Saizou : skorzystaj z nierówności o średnich teraz np. am≥gm

Radek: I to jest prawidłowo ? Nie trzeba pisać żadnych komentarzy ?

Saizou : ech czemu napisałem am≥gm miało być am≥hm

m+n		2
	≥
2		1   1   + m   n

1		1
	+		≥4
m		n

Mila: Po wykonaniu przekształceń równoważnych otrzymano nierówność prawdziwą, zatem nierówność:

1		1
	+		≥4 jest prawdziwa dla podanych założeń.
m		n

Możesz wykażać inaczej, jak radzi Saizou. Jednak chyba będzie to trudniejsze.

Radek: A to nie jest tak, że to powinno się przepisywać od końca ? Zrobić na brudno i potem przepisać ? Tak czytałem.

Saizou : na poziomie LO, co jest dziwne, można wychodzić od tezy, ale wtedy ładniej wygląda dowód nie wprost n. dla Twojego zadania, Dowód nie wprost zakładam że teza jest fałszywa, czyli

1		1
	+		<4
n		m

m+n
	<4
mn

1<4mn

1		m+n		1
	<mn co jest sprzeczne, bo		≥√mn→		≥mn,
4		2		4

zatem Teza jest prawdziwa

Mila: Radek, zadania nie uznają , bo uczniowie wychodzą od tezy i wykazują ,że założenia są prawdziwe. Ty masz przekształcenia równoważne i wykazaną prawdziwość nierówności dla danych założeń.

Radek: Dobrze dziękuję

Mila: Pamiętaj nie wykazujesz, że założenia prawdziwe, tylko z nich korzystasz, wyciągasz wnioski. Podaj w którym miejscu były wykorzystywane założenia.

Mila: No i jak klasówka, trudna była?

Radek: Zadania maturalne, nie zrobiłem 3 nierówności typu uzasadnij.. Ale dziękuję, że Pani pyta

Mila: To napisz jakie, abyś się nauczył, bo mogą być na maturze. Będziesz miał próbną maturę?

Radek: Miałem już dwie próbne matury, mam podobnież mieć jeszcze jedną w marcu.

Radek: Jutro wstawię teraz robię tę nierówności i czasmia zrobię a nie wiem czy dobrze

Radek: Wykaż, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność: x⁴−x³+2x²−x+1> 0 . x⁴−x³+x²+x²−x+1>0 x²(x²−x+1)+(x²−x+1)>0 (x²−x+1)(x²+1)>0 Δ<0 Δ<0 Brak pierwiastków ? Jaki dać komentarz ?

Eta: x²+1 >0 dla każdego x∊R i x²−x+1 >0 dla każdego x∊R , bo brak miejsc zerowych i parabola ramionami do góry to (x²−x+1)*(x²+1) >0 dla x∊R

Radek: A czy mogła by Pani jeszcze pomóc mi w kilku zadaniach ?

Mila: Pisz, pomożemy. Albo ja albo Eta.

Eta:

Mila: Eto Jak dzisiaj głowa? Pogoda sprzyja?

Eta: Witaj Mila O tak, dzisiaj już jest ok

Radek: Uzasadnij, że jeżeli a,b,c,d są liczbami dodatnimi to (a+b)(c+d)≥4√abcd. (a+b)(c+d)≥4√abcd (ac+ad+bc+cd)²≥4abcd Tędy droga ?

Eta: Wskazówka : a+b≥2√ab i c+d≥2√ab i pomnóż stronami ( bo obydwie strony dodatnie)

Saizou : skorzystaj z nierówności o średnich am≥gm a+b≥2√ab c+d≥2√cd −−−−−−−−−−−−−−−mnożąc stronami bo L i P≥0 (a+b)(c+d)≥4√abcd

Eta:

Radek: Nie znam tych zależności i nie wiem kiedy ich uzywać więc wolę inne sposoby.

Saizou : Eta jednak średnie nie idą na marne xd

Eta: No to tak: (√a−√b)²≥0 ⇒ a−2√2ab+b ≥0 ⇒ a+b≥2√ab

zombi: Ewentualnie jak nie znasz nierówności Cauchy'ego możesz na chama, tzn. (a+b)(c+d) ≥ 4√abcd ac + ad + bc + bd ≥ 4√abcd (√ac)² − 2√abcd + (√bd)² + (√ad)² − 2√abcd + (√bc)² = (√ac−√bd)² + (√ad − √bc)² ≥ 0 Chyba się nie machnąłem

Radek: Ale ja tam nie mam (√a−√b)² ? więc skąd się to bierze ?

zombi: Sorki Eta nie wiedziałem, że piszesz, bo sam byłem w trakcie

Radek: Może ktoś wytłumaczyć bez podawania całego rozwiązania od A do Z ? Takie rozwiązanie to mogę znaleźć w internecie...

Eta: Radek nie denerwuj się Takie zależności trzeba znać: bo są bardzo pomocne przy tego typu dowodach np: a²+b²≥2ab lub podobnie a+b ≥2√ab

Radek: Nie denerwuję się tylko proszę o wyjaśnienie. Jak ktoś napisze mi gotowca bez wyjaśnienia to ja nic nie zrozumiem. Ktoś to umie to napisze i do niego jest wszystko jasne, a ja nie rozumiem i dlatego nie chcę gotowców, bo chcę się nauczyć. Ale skąd tam (√a−√b)² ?

zombi: Eta podała to jako przykład, tylko zamiast a i b musisz dobrać takie liczby, że pasowało do twojego zadania. Patrz na moje rozwiązanie.

Eta: Z takiej zależności (√a−√b)²≥0 −−− która jest zawsze prawdziwa dla a>0 i b>0 otrzymujesz: a−2√ab+b²≥0 , a z niej masz prawdziwą zależność a+b≥2√ab

	a+b
a z niej ,że		≥√ab −−−− to jest nierówność między średnimi am−gm
	2

o której pisał Ci Saizou

Radek: a czemu nie np (√c−√d)² ?

Saizou : ale liczby a,b są umowne równie dobrze mogą być ś,ć ≥0

Eta: No i identycznie (√c−√d)²≥0 ⇒ c+d≥2√cd tak samo dla każdych innych literek >0 np: (√x−√y)²≥0 ⇒ x+y≥2√xy , dla x, y >0 jasne już?

Radek: A w tym zadaniu może być (√a−√c)² i (√b−√d)² ?

Mila: Radek, stosujemy różne zależności . Znasz wzory skróconego mnożenia. (a−b)²≥0 dla a,b∊R ta nierówność jest oczywista. ⇔a²−2ab+b²≥0⇔ a²+b²≥2ab Popatrz co napisała Eta My chcemy mieć wyrażenie z pierwiastkiem z prawej strony (√a−√b)²≥0 rozwijamy a−2√ab+b≥0 a+b≥2√ab skorzystałeś z wzoru skróconego mnożenia dla takich dwóch wyrazów aby pasowało do Twojego problemu. podobnie (√c−√d)²≥0⇔ c+d≥2√cd (a+b)*(c+d)≥2√ab*2√cd (a+b)*(c+d)≥4√a*b*c*d Cnw. II sposób Może prościej skorzystac z tego, że :

a+b
	średnia arytmetyczna liczb a i b jest większa lub równa od średniej geometrycznej
2

tych liczb √a*b co zapisujemy:

a+b
	≥√ab
2

a,b,c,d∊R₊

a+b
	≥√ab /*2
2

c+d
	≥√cd /*2
2

a+b≥2√ab c+d≥2{cd} mnozymy stronami (są dodatnie) (a+b)*(c+d)≥4√a*b*c*d cnw

Radek: Dziękuję, tylko ja bym nigdy nie pomyślał o takim rozwiązaniu zadania.

Eta:

Mila: O jakim?

Radek: O rozwiązaniu ze średnimi.

Mila: A przecież znasz tę zależność? Czy zapomniałeś?

3+12
	=7,5
2

√3*12=√36=6 7,5>6

Radek: Średnia arytmetyczna jest większa od średniej geometrycznej.

Saizou : kw≥am≥gm≥hm (zapiszę to teraz dla 2 składników a,b)

	a2+b2		a+b		2
√		≥		≥√ab≥
	2		2		1   1   + a   b

Radek: Wykaż, że jeżeli α jest kątem ostrym spełniającym warunek tg²α−3=0 to sinα > co sα .

sin2
	−3=0 / cos2α
cos2α

sin²α−3cos²α sin²α−3−3sin²α=0 Dobrze to zacząłem

Saizou : w sumie tak możesz, wyliczyć sinus i cosinus i porównać xd

Saizou : ale łatwiej tg²α=3 ltgαl=√3 a skoro α jest kątem ostrym to α=60^o

Radek: −2sin²α−3=0 2sin²α=−3

	3
sin2α=−		?
	2

Saizou : ale masz źle

sin2x
	−3=0
cos2x

sin²x−3cos²x=0 sin²x−3(1−sin²x)=0 sin²x−3+3sin²x=0 4sin²x=3

Radek: Dzięki

Mila: x∊(0,90⁰) tg²(x)−3=0⇔ (tgx−√3)*(tgx+√3=0 i tgx>0⇔

	π
tgx=√3⇔x=
	3

	π		√3		1		π
sin		=		>		=cos
	3		2		2		3

Radek: To to ma być równanie czy nierówność ?

Mila: Z równania obliczasz x (kąt) , potem sinx, cosx i wykazujesz nierówność.

Saizou : z równania otrzymasz kąt α=60^o a potem pokazujesz że sin60>cos60

Radek: czyli mam wyliczać i sin i cos ?

Saizou : tak

Radek: A może ktoś pokazać interpretację graficzną nierówności logarytmicznych ? na dowolnym przykładzie ?

Radek: Uzasadnij, że jeśli liczby rzeczywiste a,b,c spełniają nierówności 0 < a < b < c , to

a+b+c		a+b
	>		/6
3		2

2a+2b+2c>3a+3b −a−b+2c>0 ?

Saizou : z założenia a<c b<c −−−−−−+ a+b<2c

Radek: a takie coś może zostać ? −a−b+2c<0?

Saizou : ale skąd wiesz że to jest prawdziwe?

Radek: a to skąd wiem a+b<2c ?

zombi: Z założeń Saizou ci to rozpisał.

Radek: Udowodnij, że dla dowolnego kąta ostrego α prawdziwa jest nierówność sinα < tgα

	sinα
sinα<		/ cosα
	cosα

sinαcosα<sinα sinαcosα−sinα<0 sinα(cosα−1)<0 ?

Saizou : jakie wartości przyjmuje sin i cos dla α∊(0: 90⁰)

Radek:

1		√2		√3
	,
2		2		2

Saizou : sorry to nie tutaj miało być zobacz na wykres

Mila: 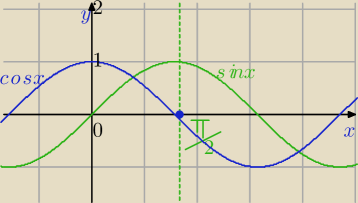f(x)=sin(x) g(x)=cos(x)

	π
Obydwie funkcje dla x∊(0,		) przyjmują wartości dodatnie. y∊(0,1)
	2

Teraz pomyśl, czy ta nierówność jest prawdziwa i dlaczego? sinα*(cosα−1)<0

Saizou : Mila mogłabyś usunąć mój post z 20:00

Radek: Nie wiem czemu ?

Saizou : sinx i cosx dla x∊(0:90) jest z przedziału (0:1) a cosx−1 dla x∊(0:90) jest <0 zatem iloczyn dwóch liczb przeciwnych jest <0

Mila: Radek uzupełniam zapisy Saizou cosx<1⇔cosx−1<0 sinx>0 Iloczyn liczb o różnych znakach jest liczbą ujemną. Popatrz na wykres.

Radek: Udowodnij, że dla dowolnych liczb dodatnich a,b,c i d prawdziwa jest nierówność ac + bd ≤ √a²+b²*√c²d² /² a²c²+2abcd+b²d²≤(a²+b²)(c²+d²) −a²d²+2abcd−b²c²≤0 / (−1) a²d²−2abcd+b²c²≥0 (ad−bc)²≥0 C.N.W?

bezendu: ok jest

Radek:

	a		1		2a
Wykaż, że jeżeli a > 0 ,		+		≥
	2		2a2		a3+1

2a3+3		2a
	≥
4a2		a3+1

(2a³+3)(a³+1)≥2a*4a² 2a⁶+2a³+3a³+3−8a²≥0 2a⁶−5a³−8a²+3≥0

Radek: ?

zawodus: 2 linijka już źle dodałeś

Radek: Fakt, dzięki

Radek: Udowodnij, że dla każdej liczby naturalnej n większej od 1 prawdziwa jest nierówność

2n 2		n 1
	>2*

(2n−2)!*(2n−1)*(2n)
	>2n
(2n−1)!*2

4n2−4n
	>2n
2

2n²−2n>2n 2n²−4n>0 n²−2>0 (n−√2)(n+√2)>0

Mila: Błędy w przekształceniu.

Radek: Tzn w którym miejscu ?

Mila:

2n 2		(2n)!		(2n−2)!*(2n−1)*(2n)
	=		=		=
		(2n−2)!*2		(2n−2)!*2

=(2n−1)*n

Radek: 2n²−n−2n>0 2n²−3n>0 n(2n−3)>0 ?

aaagaaa: Przepraszam że się wtrącę, ale bardzo potrzebuje.. https://matematykaszkolna.pl/forum/238838.html

Radek: ?

Mila: No rozwiąż nierówność w zbiorze N₊, sprawdź z założeniem.

Radek: ale tu jest parabola ?

Mila: No to co? nie umiesz rozwiązywać nierówności kwadratowych? W czym problem?

Piotr 10: Po co tak, możesz od razu z założenia zauważyć , że n > 0, z założenia 2n−3 > 0 gdyż wiemy, że z założenia n > 1

Radek: Umiem, ale to wszystko w tym dowodzie ?

Mila: Radek , widzisz prawdziwość nierówności? (patrz komentarz Piotra)

Radek: Wiem jak to rozwiązać ale nie widzę tutaj nic.

Mila: n*(2n−3)>0 i (n∊N₊ i n>1)

	3
n<0 lub n>		i n∊N+ i n>1⇔
	2

n∊{2,3,4,5,...} Wykazałeś,że Pierwsza nierówność jest prawdziwa dla (n∊N₊ i n>1)

Radek: czemu n<0

Mila: rozwiązanie nierówności: n(2n−3)>0 parabola skierowana do góry

	3
n<0 lub n>		ale n<0 nie odpowiada założeniom, bo n∊N+, to ten przypadek odrzucamy.
	2

Radek: Chyba rozumiem, dziękuję.

Mila: Załóż nowy wątek.