Plani bezendu: Uzasadnij, że suma kątów wewnętrznych dowolnego n –kąta wypukłego jest równa (n − 2 )⋅180^∘ . ?

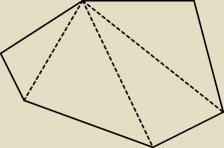
wredulus_pospolitus: wskazówka: dowolny n−kąt wypukły można podzielić na (n−2) trójkąty, których wspólnym wierzchołkiem będzie jeden z wierzchołków wielokąta wypukłego

Marcin: A że każdy trójkąt ma 180st, to pięknie wychodzi (n−2)180.

bezendu: I tyle wystarczy ? Dziwny coś ten dowód.

pigor: ... , tak wystarczy, bo nikt ci przecież nie każe dowodzić (wtedy musiałbyś indukcją) tylko uzasadnić i już . ...

Marcin: No bo jak dla mnie nie ma tutaj czego dowodzić

pigor: ... , jest co dowodzić, mianowicie to, że podany wzór S_n=(n−2)*180^o jest prawdziwy ∀n∊N i n>2 i i robi się to indukcyjnie, ale tu uzasadnienie wystarcza na poziomie szkolnym, a wzór jest wtedy po prostu tylko fajnym narzędziem , ale ciągle (... hipotezą, którą można udowodnić .

bezendu: Dziękuję.

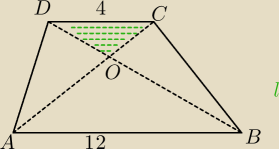
Mila: Zadanie dla bezendu Dane na rysunku:AB||DC P_ΔDOC=4cm² Oblicz pole trapezu.

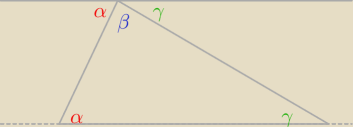
Ajtek: Prosty dowód na sumę kątów w Δ. α+β+γ=...

Saizou : P_ABCD=64?

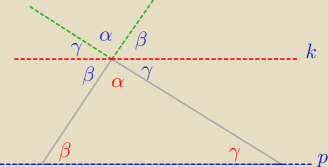
bezendu: Najpierw dowód od Ajtka 2α+2β+2γ=360⁰α p||k α+β+γ=180⁰ C.N.W

Mila: Saizou,Tobie proponuję tam. https://matematykaszkolna.pl/forum/238310.html

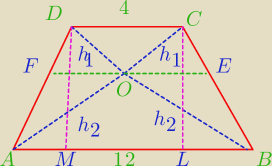
bezendu: |EF|=8

	12
skala podobieństwa k=		=3
	4

h₂=3h₁ h₂=3*2=6cm h=h₁+h₂=8cm

	4+12
P=		*8=64cm2
	2

Saizou :

Eta: P(tr)= (k+1)²*P(DOC)= (3+1)²*4= 64

bezendu: Magiczny trapez Ety

Saizou : dokładnie

Eta:

Eta: P₂=P(DOC)=4 , P₁=k²*P₂=36 P(tr)=(√P₁+√P₂)²= (2+6)²= 64

Saizou : Eta kiedyś pokazywałaś skąd to się wzięło, ale nie mogę tego znaleźć

bezendu: Tu powinna być osobna zakładka do takich wzorów żeby można sobie klikać w każdej chwili

Eta: https://matematykaszkolna.pl/szukaj/szukaj.py

Saizou : już znalazłem xd

Antek: wpisz trapezy Eta i masz linki

bezendu: Ja już sobie wydrukowałem posty Ety dotyczące trapezu

Mila: Po co liczyłeś EF?, zresztą źle policzyłeś.

bezendu: właśnie nie wiem po co

Mila: Oblicz.

bezendu: EF=6 To EF to miało być h ale najpierw inaczej zapisywałem, przepraszam za błąd.

matyk:

miecio: dajcie linka bo mój telefon nie szuka

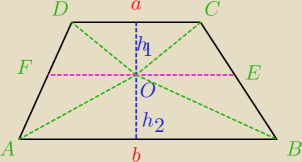
Eta: Dla bezendu W trapezie o podstawach a i b poprowadzono odcinek EF równoległy do podstaw i dzielący pole trapezu na pół. Wyznacz długość tego odcinka.

bezendu:

	a+b
h1=
	a

	b		a+b
h2=		*
	a		a

	a+b2
h2=
	a2

	a2+ab+b2
H=
	a2

Mila: 6 ze średniej harmonicznej.

bezendu: Dziękuję za zadania, zaraz wrzucę kilka swoich jeszcze

Mila: Bezendu, co to jest 20:01 ?

bezendu: odp do zadania Ety ?

Mila: No zobaczymy co Ci powie .

bezendu:

	2ab
Chyba powinno wyjść tak jednak s=		?
	a+b

Mila: Nie. A gdzie skorzystałeś z tego, że pola są równe?

bezendu: Nie skorzystałem z tego.

Eta:

Eta: @bezendu ... ja wciąż czekam na poprawne rozwiązanie

bezendu:

	ab+b2
Ostatnia szansa
	a

Eta:

zawodus: to może :

√a2+b2
√2

mogłem się pomylić w rachunkach

Eta: Skoro jesteś "zawodus" to....bardziej elegancko

	a2+b2
|EF|=√		−−−− średnia kwadratowa długości podstaw
	2

zawodus: Dajmy się wykazać bezendu Ja idę na film Eta

Eta:

Eta: @bezendu ...... ja wciąż czekam,że podasz rozwiązanie

bezendu: A co ja mam podawać skoro zrobił to zawodus ?

Eta: Zawodus podał wynik ......... a Ty masz podać pełne rozwiązanie !

bezendu: Dobrze, obiecuję, że jutro to dokończę bo dziś już nie mam siły na myślenie.

Eta: Ok .... ?

bezendu: Pierwsze po lewej

Eta: ok

bezendu: Dobranoc

Eta: Miłych snów

wredulus_pospolitus: A tak wracając (bo mnie nie było ) do zadanka z początku czyli z 16:01. Dowód 'wskazówki' jest prozaicznie prosty, wystarczy chwilkę pomyśleć: 1) w wielokącie wypukłym każdy wierzchołek można połączyć z każdym innym wierzchołkiem (co wynika wprost z definicji figury wypukłej) 2) Wybrany wierzchołek można połączyć z każdym innym wierzchołkiem za pomocą nieprzecinających się prostych (co także wynika z definicji figury wypukłej −−− łatwo wykazać, że gdyby to nie zachodziło, to figura nie może być wypukła) 3) w takim razie mamy (n−1) linii <wliczając boki> 4) wykazujemy, że w ten sposób (dokładając pozostałe boki) powstaje n−2 trójkąty c.n.w.

wredulus_pospolitus: można też zadanie to zrobić w inny sposób "każdy n−kąt wypukły można podzielić na dokładnie 'n' trójkątów taki, że: 1. Będą miały wspólny wierzchołek, będący punktem wewnątrz tegoż n−kąta 2. Pozostałymi dwoma wierzchołkami będą wierzchołki n−kąta 3. Każdy trójkąt będzie miał dokładnie jeden bok, będący jednocześnie bokiem n−kąta" W ten sposób otrzymujemy n, trójkątów ... stąd ∑kątów = n*180 −'coś' a to 'coś' to będzie 360^o ... czyli suma kątów przy wspólnym wierzchołku ... suma ta tworzy pełen okrąg = 360^o = 2*180^o c.n.w.

bezendu: Dzięki wredulus ale już nie musiałeś pisać

Radek: Skąd pochodzą te dowody z planimetrii ?

bezendu: Zbiór Kiełbasy.