koło k
Matejko: Koło K 1: x2+y2+12x+2y+21 <= 0 przesuwamy o wektor v=[4,4] i otrzymujemy koło K 2.
Oblicz pole części wspólnej tych kół.
Obliczyłam, że K2: (x+2)2+(y−3)2=16 czyli środek drugiego koła O=(−2,3). Ale jak
obliczyć część wspólną tych kół?
20 lut 20:05
Matejko: up
20 lut 20:36
Matejko: up
20 lut 20:42
Mila:
x
2+y
2+12x+2y+21 ≤ 0⇔
(x+6)
2−36+(y+1)
2−1+21≤0
(x+6)
2+(y+1)
2≤16 S
1=(−6,−1) r=4
S
1=(−6,−1)→T
[4,4]→S
2(−2,3) r=4
(x+2)
2+(y−3)
2≤16
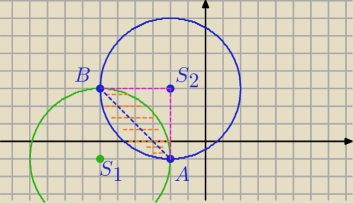
Punkty przecięcia okręgów: ( tu widać, ale sprawdzimy)
(x+2)
2+(y−3)
2=16
(x+6)
2+(y+1)
2=16 po rozwiązaniu
B: x=−6, y=3
A: x=−2 ,y=−1
ΔAS
2B − Δprostokątny.
| 1 | | 1 | | 1 | |
| Psoczewki= |
| *π*42− |
| *4*4 |
| 2 | | 4 | | 2 | |
20 lut 20:46
20 lut 20:54
20 lut 20:54
Mila:
Bezendu, tam jest inny okrąg. Istotne jest w jakich punktach przecinaja się okręgi.
Tu łatwo można obliczyć pole wycinka koła i pole Δ.
20 lut 21:07
bezendu: Ale tam jest podobne zadanie i dlatego wstawiłem link.
20 lut 21:08
Matejko: pole mi wyszło 8π−8 a ma być 8π−16 dlaczego?
wzór dobry? Taki mam:
P=2*14πr2−12r2
21 lut 14:28
Mila:
20:46 masz napisane , że to pole połowy soczewki.
Poprawiam Twój wzór:
P=2*(4π−8)=8π−16
21 lut 14:46
Matejko: aha dziękuje bardzo
21 lut 14:51
Mila:
21 lut 15:08