jerey: wyznaczyc rowania stycznych do okregu o rowaniu x²+y²=4 S(0,0) r = 2 na oko widac y=x+4 y=x−4 robiłem sposobem; rowanie prostej to; y=ax+b r=2 s(0,0) prosta przechodzi przez punkt (0,4) ⇒ 4=a*0+b⇒b=4 rowanie prostej y=ax+4 stąd podstawiam do długosci odcinka bo chce wyliczyc a rowanie ogolne prostej ax−y+4=0

	a*0+(−1)*0+4
2=		takie dziwactwo mi wychodzi w odpowiedziach mam
	√2

ze proste mają rowanie postaci y=√3x+4 i −√3x+4 chodzi mi o to jak obliczyc ten wspolczynnik kierunkowy ?

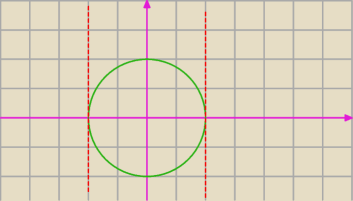
Radek: x=2 lub x=−2

jerey: sory nie dodałem ze styczne mają przechodzic przez punkt P=(0, 4)

bezendu: No właśnie x²+y²=4 S=(0,0) r=2 y=ax+b P=(0,4) y=ax+4 x²+(ax+4)²=4 x²+a²x²+8ax+16−4=0 x²+a²x²−8ax+12=0 x²(a²+1)−8ax+12=0 Dokończ

jerey: Δ=0 czyli 8a²−4(a²+1)*12 i to rozwiazac tak?

Radek: https://matematykaszkolna.pl/forum/231726.html

jerey: dzieki radek mecze sie juz z tym prawie 2 godziny robie roznymi sposobami te zadania ni nic . przydalo sie