Ge
Radek:
Wytłumaczy ktoś jak pisać równanie stycznych do okręgu przechodzących przez jakiś punkt ?
13 sty 19:10
Mila:
Różnie można. Zależy od typu zadania.
Napisz jakie masz typy.
13 sty 19:13
Radek:
(x+1)2+(y−1)2=5 i styczne przechodzą przez punkt A=(2,0)
13 sty 19:14
Ewa: Styczna jest prostopadła to promienia, z którym się styka, czyli korzystasz ze wzoru na
wyznaczenie współczynnika kierunkowego przy prostych prostopadłych. Jak masz już współczynnik,
to wstawiasz to wszystko do wzoru: równanie prostej przechodzącej przez pkt ... , o
współczynniku a

13 sty 19:21
Radek:
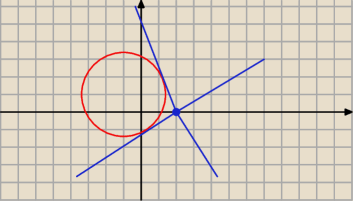
?
13 sty 19:23
Radek: ?
13 sty 19:30
Radek: Pomoże ktoś ?

13 sty 19:37
Ewa: Myślę cały czas...
13 sty 19:39
Radek: Pani Milu może mi Pani to wytłumaczyć ? Błagam.
13 sty 19:44
ICSP: y = ax + b − równanie stycznej zatem
0 = 2a + b
czyli styczna ma równanie :
y = ax − 2a
y = ax − 2a
(x+1)2 + (y−1)2 = 5
Masz taki układ równań. Teraz trzeba odpowiedzieć na pytanie : ile punktów wspólnych ma styczna
z okręgiem i rozwiązać odpowiednio układ równań.
13 sty 19:45
Radek:
Jeden punkt wspólny.
13 sty 19:47
ICSP: No to dalej już bez problemu.
13 sty 19:49
Radek:
Podstawić za y ax−2a ?
13 sty 19:50
Mila:
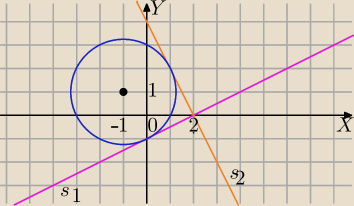
Rozwiąż sposobem
Ewy
II sposób:
s: styczna
y=ax+b i A∊s,
0=2a+b
b=−2a
s: y=ax−2a
Przekształcam na postac ogólną
ax−y−2a=0
S=(−1,1)
Korzystam , że odległość stycznej od środka okręgu jest równa r=
√5
| | |a*(−1)−1−2a| | |
√5= |
| ⇔|3a+1|=√5*√a2+1 /2⇔ |
| | √a2+1 | |
2a
2+3a−2=0
Δ=25
s
2:y=−2x+4
13 sty 19:53
ICSP: Witaj
Eta 
Jakoś nigdy nie lubiłem tego wzoru

13 sty 19:54
ICSP: Mila oczywiście

13 sty 19:54
Radek:
A trzeba korzystać z tej stycznej do środka okręgu i ze wzoru na długość odcinka ?
13 sty 19:58
Mila:
ICSP, polemizowałabym.
y = ax − 2a
(x+1)2 + (y−1)2 = 5
(x+1)2 + (ax−2a−1)2 = 5 i tu dla wielu uczniów pojawia się problem z tym drugim kwadratem,
Liczę dla Radka
x2+2x+1+a2x2+4a2+1−4a2x−2ax+4a=5 porządkuję
x2*(a2+1)+x(2−4a2−2a)+(4a2+4a−3)=0 poddaję się.
13 sty 20:21
Radek:
Chyba sobie odpuszczę tę maturę roz. Bo analityczna to nie moja bajka. A za rozwiązanie
dziękuję.
13 sty 20:23
Mila:
Radek, nie panikuj. Spokojnie czytaj, analizuj.
13 sty 20:25
Radek:
Analizuję ale i tak wszystkich zadań nie rozumiem a mało czasu już.
13 sty 20:32
ICSP: Fakt. Zły pomysł miałem

13 sty 20:36
Radek:
A skąd wzięła się 3 linijka. ?
13 sty 20:56
matyk: ICSP pomysł jest dobry, a to że rachunki czasem mogą wyjść trudne to inna sprawa

13 sty 21:02
Radek: ?
13 sty 21:13
Mila:
Radek , o jaką linijkę Ci chodzi, dokładnie podaj.
13 sty 21:13
13 sty 21:15
Mila:
s: styczna
y=ax+b i A∊s,
0=2a+b
b=−2a
s: y=ax−2a
Obliczone a wstawiam do wzoru : y=ax−2a
13 sty 21:27
Radek:
Dziękuję jeszcze mam kilka przykładów.
13 sty 21:28
Mila:
Pisz.
13 sty 21:34
Radek:
Dany jest okrąg o równaniu x2+y2−10x+4y+25=0 . Napisz równania stycznych do tego okręgu,
przechodzących przez początek układu współrzędnych
(x−5)2−25+(y+2)2−4+25=0
(x−5)2+(y+2)2=4
y=x
i dalej na długość odcinka ?
13 sty 21:38
Mila:
zrób rysunek , jedną styczną zobaczysz
Tu zrobisz I sposobem, jak [Z[ICSP i Ewa radzili]
y=ax i podstawiasz do równania (x−5)2+(y+2)2=4
Potem Δ=0
13 sty 22:02
Radek:
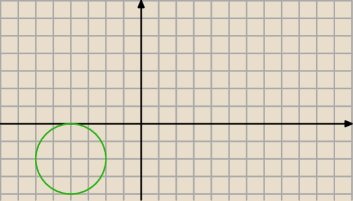
A czemu nie można Pani sposobem ?
13 sty 22:05
Mila:
Oczywiście można , ale teraz prościej tamtym, zrób dwoma sposobami
styczna
y=ax
ax−y=0
d=r=2
dokończ i napisz tu.
13 sty 22:07
Radek:
y=ax
(x−5)2+(y+2)2=4
(x−5)2+(ax+2)2=4
x2−10x+25+ax2+4ax+4−4=0
x2−10x+25+ax2+4ax=0
(1+a)x2−(10+4a)x+25=0
o to chodzi ?
13 sty 22:11
Mila:
Masz tam błąd:
(x−5)2+(ax+2)2=4
x2−10x+25 +a2x2+4ax+4=4
x2*(1+a2)+x*(4a−10)+25=0
13 sty 22:31
Radek:
(4a−10)2−4*(1+a2)*25=0
i znowu wyjdzie a2 chyba Pani rozwiązanie o wiele lepsze.
13 sty 22:32
Mila:
Wszystko dobrze, dokończ .
13 sty 22:53
Radek:
Znowu Δ mam liczyć ?
13 sty 22:55
Radek: ?
13 sty 23:02
Mila:
Masz rozwiązać to równanie.
16a
2−80a+100−100−100 a
2=0
−84a
2−80a=0
−a(84a+80)=0
a=0 lub 84a=−80
| | 80 | | −20 | |
a=0 lub a=− |
| = |
| |
| | 84 | | 21 | |
y=ax
y=0*x⇔y=0 (oś OX)
13 sty 23:09
Radek:
Dziękuję. Rozwiązałem pierwszym sposobem.
13 sty 23:11
Radek:
Mam okrąg o środku S=(−2,3) i promieniu 2
trzeba wyznaczyć styczne przechodzące przez punkt A=(−1,0)
x=0
Ale może ktoś pokazać tym sposobem na długość odcinka jak to zrobić ?
14 sty 20:36
Mila:
Co to znaczy na długość odcinka?
14 sty 20:37
Radek:
odległość punktu od prostej.
14 sty 20:44
Radek: ?
14 sty 21:05
Mila:
No dobrze, podpowiem:
Styczna ma równanie:
s:y=ax+b i punkt A należy do tej stycznej⇔0=−a+b⇔b=a
s: y=ax+a przekształcam na postać ogólną:
ax−y+a=0
Teraz podstaw ładnie do wzoru na odległość punktu S od tej prostej.
14 sty 21:05
Radek:
No to mam
| | −ax+y+1| | |
2= |
| S=(−2,3) |
| | √1+a2 | |
U{2a+3+1}{
√a2+1=2
i tutaj nie wiem jak dalej sobie poradzić
|2a+4|=2*
√a2+1 /
2
4a
2+16a+16=4a
2+4
16a=−12
I nie wyszło poprawnie

14 sty 21:12
bezendu:
dobrze wyszło.
14 sty 21:25
Radek: ?
14 sty 21:35
Mila:
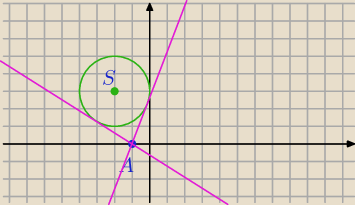
ax−y+a=0, S=(−2,3)
Teraz oblicz, bo błędnie podstawiłeś.
14 sty 21:41
Radek:
Czemu błędnie ?
mam prostą y=ax+b i przechodzi przez punkt A=(0,−1)
−1=a*0+b⇒b=−1
y=ax−1
−ax+y+1=0
S=(−2,3)
|2a+4|=2*
√a2+1 gdzie jest błąd ?
14 sty 21:46
Radek: ?
14 sty 22:11
Mila:
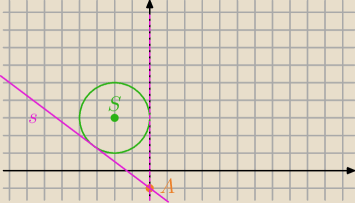
Przecież przedtem (20:36) napisałeś A=(−1,0) to jak w końcu ma być?
Jeżeli A=(0,−1), to masz dobrze.
s:y=ax−1
Jedna styczna to :
x=0 (Oś OY)
| | −3 | |
s: y= |
| x−1 druga styczna |
| | 4 | |
14 sty 22:19
Radek:
(0,−1) Przepraszam
14 sty 22:24
Mila:
No to masz dobrze, coś jest niejasne?
14 sty 22:25
Radek:
Wszystko już jasne ale jeszcze z jednym mam problem.
14 sty 22:26
Radek:
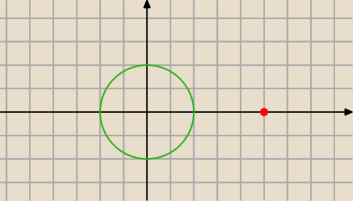
Z punkt A=(5,0) poprowadzono styczne do okręgu o równaniu x
2+y
2=4 wyznacz tang pod którym
przecinają się te proste
y=ax+b
0=5a+b ⇒b=−5a
y=ax−5a
−ax+y+5a=0
|5a|=
√a2+1*2 /
2
25a
2=4a
2+4
21a
2=4
| | 2√21 | | 2√21 | |
a= |
| lub a=− |
| |
| | 21 | | 21 | |
ok jak na razie ?
14 sty 22:32
Mila:
Tak.
14 sty 22:43
Radek:
I teraz tym wzorem z tablic ?
Ale tam mam dla kata ostrego ?
14 sty 22:47
Mila: Z punktu A=(5,0) poprowadzono styczne do okręgu o równaniu x2+y2=4 wyznacz tangens kąta pod
którym przecinają się te proste.
y=ax−5a
Liczysz tg połowy kąta , Oś X jest osią symetrii
| | α | | | | 2√21 | |
liczysz tg |
| = |
| = |
| |
| | 2 | | 5 | | 21 | |
potem wzór na podwojony tangens kąta.
14 sty 23:03
Radek:
Tego to już nie dokończę bo nie wiem jak.
14 sty 23:04
Mila:
Zadanie można prościej zrobić, jutro pokażę, a może Eta, tu spojrzy to Ci napisze.
(poproś!)
Dobranoc.
14 sty 23:05
Radek:
Dobranoc i dziękuję

14 sty 23:06
Eta:
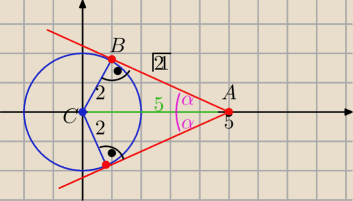
| | 2 | | √21 | |
|AB|=√52−22= √21 , sinα= |
| , cosα= |
| |
| | 5 | | 5 | |
sin(
2α) = 2sinα*cosα=..........
cos(
2α)= 1−2sin
2α=....
| | sin2α | |
tg(2α)= |
| =........... |
| | cos2α | |
| | 2tgα | |
to ze wzoru : tg(2α)= |
| =.......... |
| | 1−tg2α | |
15 sty 01:03
bezendu:
Czemu tutaj właśnie z podwójnego kąta ? Nie można z tego wzoru z tablic ?
15 sty 01:08
Eta:
Ja,tak lubię

15 sty 01:10
15 sty 01:13
bezendu:
Dzięki Eta ale czy ten wzór nie jest tylko dla kąta ostrego ?
15 sty 12:40
Radek:
Dziękuję. A właśnie to nie obi się tym wzorem 01;13 ?
15 sty 15:59
Radek: ?
15 sty 16:09
Mila:
Jak Wam, pięknie napisała Eta nie trzeba było szukać równań stycznych.
Podobne zadanie było na maturze, szukanie tych równań zajmuje trochę czasu.
15 sty 17:10
bezendu:
Ale można używać tego wzoru ? Nie wiadomo czy tam jest kat ostry ?
15 sty 17:12
bezendu: ?
15 sty 17:55
bezendu: ?
15 sty 18:24
bezendu:
To masz problem bo nie mam facebook'a. I radziłbym udać się do psychiatry choć może już za
późno do Ciebie.
15 sty 18:34
bezendu: ?
15 sty 18:40
Mila:
Napisz w którym miejscu zadania masz ten problem.
Połowa kąta między stycznymi jest kątem ostrym.
| | α | | 2 | | α | |
Tutaj sin |
| = |
| i dalej z jedynki tryg. obliczaj cos |
| , |
| | 2 | | 5 | | 2 | |
Potem wzór :
15 sty 18:44
15 sty 18:46
Mila:
Między przecinającymi się prostymi są dwie pary kątów wierzchołkowych,dla jednej pary masz
tangens dodatni dla drugiej ujemny.
Dla prostopadłych masz w mianowniku zero.
Z tego wzoru otrzymasz wynik dodatni, czyli dla kąta ostrego, dla rozwartego masz wynik ujemny.
dla drugiej pary kątów wierzchołkowych masz
15 sty 20:26
bezendu:
I który należy wybrać?
15 sty 20:27
Mila:
Analizujesz warunki zadania.
15 sty 20:31
bezendu:
wyznacz tang pod którym przecinają się te proste dodatni ?
15 sty 20:33
oki: Obie odpowiedzi są poprawne. Jeśli nie ma sprecyzowanej odpowiedzi wystarczy podać jedna
wartość.
15 sty 21:15
bezendu:
Dziękuję.
15 sty 21:17

 ?
?

 Rozwiąż sposobem Ewy
II sposób:
s: styczna
y=ax+b i A∊s,
0=2a+b
b=−2a
s: y=ax−2a
Przekształcam na postac ogólną
ax−y−2a=0
S=(−1,1)
Korzystam , że odległość stycznej od środka okręgu jest równa r=√5
Rozwiąż sposobem Ewy
II sposób:
s: styczna
y=ax+b i A∊s,
0=2a+b
b=−2a
s: y=ax−2a
Przekształcam na postac ogólną
ax−y−2a=0
S=(−1,1)
Korzystam , że odległość stycznej od środka okręgu jest równa r=√5
 Jakoś nigdy nie lubiłem tego wzoru
Jakoś nigdy nie lubiłem tego wzoru



 A czemu nie można Pani sposobem ?
A czemu nie można Pani sposobem ?

 ax−y+a=0, S=(−2,3)
ax−y+a=0, S=(−2,3)
 Przecież przedtem (20:36) napisałeś A=(−1,0) to jak w końcu ma być?
Jeżeli A=(0,−1), to masz dobrze.
s:y=ax−1
Jedna styczna to :
x=0 (Oś OY)
Przecież przedtem (20:36) napisałeś A=(−1,0) to jak w końcu ma być?
Jeżeli A=(0,−1), to masz dobrze.
s:y=ax−1
Jedna styczna to :
x=0 (Oś OY)
 Z punkt A=(5,0) poprowadzono styczne do okręgu o równaniu x2+y2=4 wyznacz tang pod którym
przecinają się te proste
y=ax+b
0=5a+b ⇒b=−5a
y=ax−5a
−ax+y+5a=0
Z punkt A=(5,0) poprowadzono styczne do okręgu o równaniu x2+y2=4 wyznacz tang pod którym
przecinają się te proste
y=ax+b
0=5a+b ⇒b=−5a
y=ax−5a
−ax+y+5a=0


