matematykaszkolna.pl
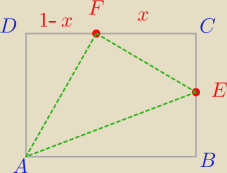
Planimetria bezendu: rysunekBok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F umieszczone tak, by |CE | = 2|DF | . Oblicz wartość x = |DF | , dla której pole trójkąta AEF jest najmniejsze. Co dalej ? chcę wskazówkę a nie gotowca którego mam dokończyć.
20 lut 00:35
Marcin: Pole tego trójkąta, to pole kwadratu odjąć pola trójkątów AFD FEC i EAB.
20 lut 00:38
bay: Na rysunku nie widzę kwadratu !
20 lut 00:39
bezendu: Dzięki emotka
20 lut 00:39
Trivial: bay, miałem mówić to samo. emotka
20 lut 00:40
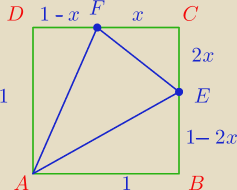
bezendu: rysunek
20 lut 00:42
Marcin: i pamiętaj że DF to x, a CE 2x emotka (robiłem już to zadanie emotka )
20 lut 00:43
bezendu: A no tak pomyliłem oznaczenia.
20 lut 00:44
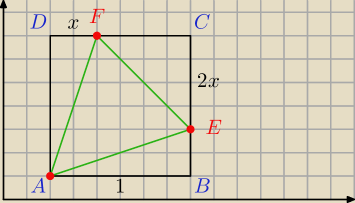
Trivial: rysunekOto właściwy rysunek. W zadaniu jest narzucone: x = |DF|.
20 lut 00:44
bezendu: I teraz muszę stworzyć funkcję kwadratową opisującą pole trójkąta AFE ?
20 lut 00:45
Trivial: Tak. To jest trywialne. Masz 3 trójkąty prostokątne i kwadrat. Jak się mają ich pola? emotka
20 lut 00:46
Marcin: 12−trzy pola trójkątów. Reszta prosto emotka
20 lut 00:46
bezendu: Dzięki i gratulację Trivial bo nie miałem jeszcze okazji emotka
20 lut 00:49
bay: Pole tego trójkąta będzie najmniejsze ⇔ jak suma pól pozostałych trzech trójkątów będzie mieć wartość największą Zbadaj maximum P(x)= P(ABE)+P(ADF)+P(EFC) =...... Dziedzina P(x) : x∊(0,12)
20 lut 00:50
Trivial: Dzięki. emotka
20 lut 00:51
bezendu:
 1 
czyli xw=
 4 
20 lut 00:52
bay: okemotka
20 lut 00:53
bezendu: Tylko mam jeszcze jedno pytanie pole pole trójkąta będzie najmniejsze jeśli pola trójkątów będzie jak największe ?
20 lut 00:55
bezendu: Proszę o sprawdzenie https://matematykaszkolna.pl/forum/238265.html
20 lut 00:58
Trivial: Można bezpośrednio obliczyć pole trójkąta AFE:
 x 1−2x 2x(1−x) x 1 
p(x) = 1 −
−
−
= x2 −
+
 2 2 2 2 2 
 1 7 
= (x−
)2 +
 4 16 
 1 
A zatem minimum dla x =
.
 4 
20 lut 01:05