plan bezendu: W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza a+b+c=14 b=2a 3a+c=14⇒c=14−3a f(x)=a²+(2a)²+(14−3a)² f(x)=a²+4a²+196−84a+9a² f(x)=14a²−84a+196 x_w=3

	13
cosα=
	15

bezendu: ?

Domel: No i jak − obliczyłeś x_w czy a_w? Czy to minimum czy maksimum funkcji? Jakie są pozostałe boki? Jak sobie odpowiesz to następnie zajrzyj tutaj https://matematykaszkolna.pl/strona/543.html

Domel: A − i jaki to wychodzi trójkąt?

bezendu: A czemu ma służyć ten link? Skoro ja znam to twierdzenie. Ja pytam o wynik czy ok?

bezendu: ?

Trivial: http://www.wolframalpha.com/input/?i=extrema+x^2+%2B+%282x%29^2+%2B+%2814-3x%29^2 Czyli a wyliczone dobrze. (a,b,c) = (3,6,5)

Domel: wg mnie to

	9 − 36 − 36		−63		7
cosα =		=		=
	−2 * 6 * 6		−72		8

Domel: (a, b, c) = (3, 6, 6)

Trivial:

Trivial:

	13
cosα =		OK
	15

Bogdan: bezendu rozwiązał poprawnie zadanie (pomijam niedociągnięcia w zapisie rozwiązania i traktuję ten zapis jak szkic rozwiązania). Szukany cosinus ma wartość 13/15.

Bogdan: Te niedociągnięcia to np.: powinno być f(a), a nie f(x) oraz a_w = 3 a nie x_w = 3

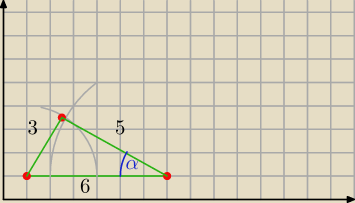
Domel: Trivial nie wiem skąd mi wyszło 14−9 = 6 Masz racją (a, b, c) = (3, 6, 5) no i

	9 − 36 − 25		−52		13
cosα =		=		=		czyli bezendu ma gut
	−2 * 6 * 5		−60		15

Domel: No i sorki bezendu za ten link na górze − został wstawiony, bo wychodził mi inny (niestety błędny) wynik

bezendu: Dziękuję Panowie.