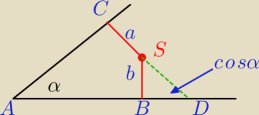
plan bezendu: Do obszaru kąta ostrego o mierze α należy punkt S , którego odległości od ramion kąta są równe a i b . Oblicz odległość punktu S od wierzchołka kąta

	b
SD=
	cosα

	bsinα
BD=
	cosα

	acosα+b
CD=
	cosα

	acosα+b−bsin2α
|AD|=
	cosαsinα

	acosα+b−bsin2α+bcosαsinα
AS=√
	sinαcosα

?

bezendu: ?

Mila: Nie myślę już, ponadto zmartwiła mnie sytuacja z Etą, tak ładnie nam się pracowało.

bezendu: Na chamstwo nie ma niestety lekarstwa.

Mila: Inny mam wynik, jutro to przeliczę jescze raz .

Janek191:

b
	= sin (90o − α) = cos α
SD

	b
czyli SD =
	cos α

BD		b
	= cos( 90o − α) = sin α ⇒ BD = SD * sin α =		* sin α = b*tg α
SD		cos α

	b		a cos α + b
CD = a + SD = a +		=
	cos α		cos α

CD		CD
	= tg α ⇒ CD = AC*tg α ⇒ AC =		⇒
AC		tg α

	a cos α + b     cos α		a cos α + b		cos α
AC =		=		*		=
	tg α		cos α		sin α

	a cos α + b
=
	sin α

oraz z Tw. Pitagorasa

	( a cos α + b)2
AS2 = AC2 + a2 =		+ a2 =
	sin2α

	a2 cos2 α + 2a*b cos α + b2		a2 sin2 α
=		+		=
	sin2α		sin2α

a2*( cos2 α + sin2 α) + 2a*b cos α + b2		a2 + b2 + 2a*b cos α
	=
sin2α		sin2α

Janek191: Czyli

	a2 + b2 + 2a*b cos α
AS = √
	sin α

=================================

Janek191: Ten pierwiastek dotyczy tylko licznika

	√ a2 + b2 + 2a*b cos α
AS =
	sin α

zawodus: A co to za sytuacja?

bezendu: Czemu wgl jest liczone OC ?

Antek: Milu dzien dobry . Pozdrawiam Eta wroci na forum . To jest silniejsze od niej

Mila: Mam taką nadzieję, Antku, musi odreagować. Wie, że czekamy . Również pozdrawiam.

Antek: Tak Milu niby starsze osoby powinny byc odporniejsze na takie docinki ale niektorych nie da sie od razu przelknac . Sam sie z takim czyms spoktykam . To ze wroci to pewne ale miejmy nadzieje ze wroci szybko

Mila: Bezendu Mogłeś AD przekształcić do prostszej postaci.

	a cosα+b(1−sin2α)		a cosα+b cos2α		a+bcosα
|AD|=		=		=
	cosα*sinα		sinα cosα		sinα

I teraz i tak wychodzą niewdzięczne rachunki. Liczyłeś AS z ΔABS? Janek liczył z górnego Δ. Ja mam inny sposób, prostsze są rachunki.

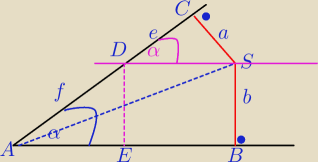
Mila: 1) w ΔSCD:

	a		a cosα
tgα=		⇔e=a ctgα=
	e		sinα

wΔAED:

	b		b
sinα=		⇔f=
	f		sinα

	a cosα		b
|AC|=e+f=		+
	sinα		sinα

	acosα+b
|AC|=
	sinα

wΔACS: |AS|²=|AC|²+a²⇔

	a2cos2α+2abcosα+b2
|AS|2=		+a2=
	sin2α

	a2cos2α+2abcosα+b2+a2 sin2α
=		=
	sin2α

	a2*(cos2α+sin2α)+2abcosα+b2
=
	sin2α

	√a2+2abcosα+b2
|AS|=
	sinα

bezendu: Ja właśnie liczyłem w ten sposób. Dziękuję.

Mila: To znaczy tak, jak ja czy Janek ? Bo zacząłeś inaczej. Tam wychodziły żmudne rachunki.

bezendu: Twoim sposobem. I dlatego zależało mi na innym rozwiązaniu niż rozwiązanie Janka.

Mila: Zobaczyłeś trapez?

bezendu: Widziałem ale nie rozumiem tego. A w tym zadaniu co czytam to ja jeszcze inaczej liczyłem bo nie używałem anie ctg ani tg

bezendu: A czemu nie można policzyć Najpierw CD,EB i potem AS ?

bezendu: ?

Mila: Możesz , ale rachunki jakie?

bezendu: Jest trochę rachunków ale |AB| już mi wychodzi nie poprawne.

Mila: Pewnie błędnie przekształciłeś. A może inna postac równoważna. Wrzuc na wolfram, czy jest true.

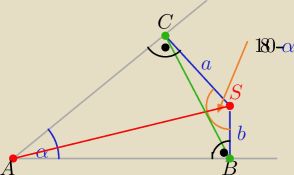
bay: Na czworokącie ABSC można opisać okrąg ( dlaczego? |<BSC|= 180^o−α Średnicą tego okręgu jest odcinek |AS|=2R (dlaczego? Z twierdzenia kosinusów w trójkącie BCS : |BC|²=a²+b²−2ab*cos(180^o−α)= a²+b²+2ab*cosα z tw. sinusów trójkącie ABC

|BC|		√a2+b2+2ab*cosα
	=2R=|AS| ⇒ |AS|=
sinα		sinα

bezendu: Dziękuję Eta za rozwiązanie ale ja chcę dojść do poprawnego rozwiązania swoim sposobem.

Mila: Też miałam na uwadze sposób z okręgiem, ale myślę, że dość prosty jest z równoległą DS. Tylko Bezendu nie czyta. Mam jeszcze jeden sposób, ale już nie mące w główce naszemu maturzyście.

bezendu: Przepraszam bardzo, ale ja czytam wszystkie odpowiedzi i staram się zrozumieć a, że nie rozumiem to inna sprawa.

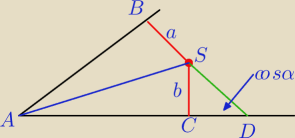
bezendu: Wstawiam jeszcze raz: Do obszaru kąta ostrego o mierze α należy punkt S , którego odległości od ramion kąta są równe a i b . Oblicz odległość punktu S od wierzchołka kąta

	b
|SD|=
	cosα

	bsinα
|CD|=
	cosα

	acosα+bsinα
|BD|=
	cosα

Czu to na razie jest poprawnie ?

Antek: Milu prosze spojrz tu https://matematykaszkolna.pl/forum/238239.html:)))))

Antek: https://matematykaszkolna.pl/forum/238239.html tak mialo byc

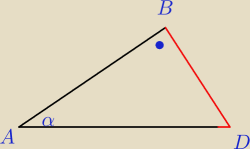
bezendu: Teraz wyliczam |AD|

	acosα+bsinα
|BD|=
	cosα

	BD
sinα=
	AD

	acosα+bsinα		1
sinα=		*
	cosα		|AD|

	acosα+bisnα
sinα=
	|AD|cosα

|AD|cosαsinα=acosα+bsinα

	acosα+bsinα
|AD|=		?
	cosαsinα

|AC|=|AD|−|CD|

	acosα+bsinα		bsinα
|AC|=		−
	cosαsinα		cosα

?

bezendu:

	acosα+bsinα−bsin2α
|AC|=
	cosαsinα

Czy AC jest dobrze wyliczone ?

bezendu: ?

Mila: Zaraz. Czekaj. Mam od tych wzorków oczopląs.

Mila: 21:19 trzeci wzór tak ma być.

	b		acosα+b
BD=a+SD=a+		=
	cosα		cosα

bezendu: Zaraz poprawię resztę.

bezendu:

	|BD|
sinα=
	AD|

	acosα+b		1
sinα=		*
	cosα		|AD|

	acosα+b
sinα=
	|AD|cosα

|AD|cosαsinα=acosα+b

	acosα+b
|AD|=
	sinαcosα

	acosα+b		bsinα
|AC|=		−
	sinαcosα		cosα

	acosα+b−bsin2α
|AC|=
	sinαcosα

Teraz ok ?

Mila: w liczniku wyłącz: =acosα+ b *(1−sin²α)=acosα+b * cos²α to uprościsz

bezendu: Może się namęczyłem ale wynik wyszedł teraz prawidłowy

Mila: Do końca? Pomyśl, że na maturze masz ograniczony czas. Wybierasz sposób najmniej czasochłonny. Trafność wyboru sposobu wypracowujesz.

bezendu: Teraz jeszcze ten dowód żeby zrozumieć

bezendu: Tak do końca wyszło ok. Ja zawsze chcę kontynuować swój pomysł, inne rozwiązanie też analizuję ale staram się zrobić według pierwszej myśli.