| |2x−0+4| | ||
d(P,l) = | = √5 | |
| √4+1 |
| I 2*x − 1*0 + 4 I | ||
d = | = √5 | |
| √22 + (−1)2 |

 Jeśli chcesz poćwiczyć ... to możesz tak ... a można znacznie prościej −
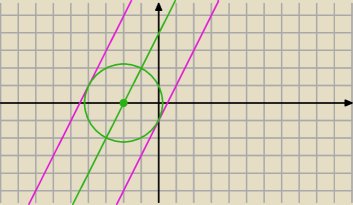
Jeśli chcesz poćwiczyć ... to możesz tak ... a można znacznie prościej − Prosta l przecina Ox w punkcie S=(−2, 0)
Punkty odległe od S o √5 leżą na okręgu (x+2)2+y2=5
Wyznaczmy styczne do tego okręgu mające współczynnik kierunkowy a=2
czyli y=2x+b
Z porównania równania okręgu i stycznych
(x+2)2+(2x+b)2=5
x2+4x+4+4x2+4bx+b2−5=0
5x2+(4+4b)x+b2−1=0
Styczna ma z okręgiem jeden punkt wspólny zatem Δ=0
(4+4b)2−20(b2−1)=0
16+32b+16b2−20b2+20=0
−4b2+32b+36=0 ⇒ b2−8b−9=0 Δ'=64+36 b1=−1 b2=9
nasze styczne mają zatem równania y=2x−1 i y=2x+9
Przecinają one oś Ox odpowiednio dla x=1/2 i x=−9/2
Prosta l przecina Ox w punkcie S=(−2, 0)
Punkty odległe od S o √5 leżą na okręgu (x+2)2+y2=5
Wyznaczmy styczne do tego okręgu mające współczynnik kierunkowy a=2
czyli y=2x+b
Z porównania równania okręgu i stycznych
(x+2)2+(2x+b)2=5
x2+4x+4+4x2+4bx+b2−5=0
5x2+(4+4b)x+b2−1=0
Styczna ma z okręgiem jeden punkt wspólny zatem Δ=0
(4+4b)2−20(b2−1)=0
16+32b+16b2−20b2+20=0
−4b2+32b+36=0 ⇒ b2−8b−9=0 Δ'=64+36 b1=−1 b2=9
nasze styczne mają zatem równania y=2x−1 i y=2x+9
Przecinają one oś Ox odpowiednio dla x=1/2 i x=−9/2