matematykaszkolna.pl
trapez bezendu: W trapezie równoramiennym ABCD ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie ABCD jest równy 34 , oblicz długości jego podstaw. mi wyszło a=2 b=18 ?
15 lut 21:42
Janek191: Ile jest równy tg kąta ostrego ?
15 lut 21:50
bezendu:
3 
4 
15 lut 21:50
Mila:
 3 
Chyba tgα=
?
 4 
Tradycyjnie dolna podstawa a, górna b. U Ciebie chyba odwrotnie?
15 lut 21:52
bezendu: Tak ja przyjąłem górną a
15 lut 21:52
Janek191: To co innego emotka a > b a + b + 2c = 40 c = 10 a + b = 40 − 2*10 =20 oraz
h 3 
= tg α =
⇒ h = 34 x ⇒ h2 = 916 x2
x 4 
x2 + h2 = c2 x2 + 916 x2 = 100
25 
x2 = 100
16 
 16 
x2 = 100*
 25 
 4 
x = 10*
= 8
 5 
2x + b = a ⇒ 16 + b = a a + b = 16 + b + b = 20 ⇒ b = 2 a = 16 + 2 = 18 Odp. a = 18 , b = 2 ==================
15 lut 22:03
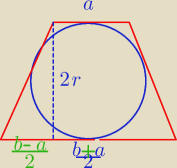
bezendu: rysunekUdowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu I dalej co robić ?
15 lut 22:12
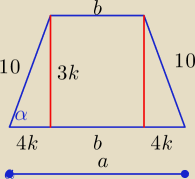
Eta: rysunek a+b=20 ⇒ 8k+2b=20 , 9k2+16k2=100 ⇒ k=2, k>0 to: 2b= 20−16 ⇒b=2 i a=18
15 lut 22:13
bezendu: już wiem jakemotka podobne zadanie jak w maju tamtego roku
15 lut 22:17
Eta: https://matematykaszkolna.pl/forum/237469.html
15 lut 22:17
bezendu: Już sam udowodniłem emotka Ale dziękuję
15 lut 22:19
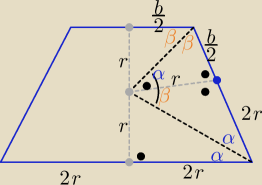
bezendu: Na okręgu o promieniu r opisano trapez równoramienny, którego długość jednej z podstaw wynosi 4r . Oblicz odległość środka okręgu od wierzchołków trapezu która ta podstawa ma 4r ?
15 lut 22:28
5-latek: Przeciez srednica okregu to 2r tylko
15 lut 22:58
bezendu: Dobra już chyba sobie poradzę emotka
15 lut 23:01
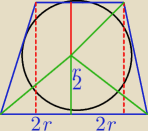
bezendu: rysunek Tak może być ?
15 lut 23:17
Mila: Tak . ΔBOC− Δprostkątny
15 lut 23:23
bezendu:
 r 
Ale czy ta wysokość trójkąta równoramiennego ( w podstawie) to
?
 2 
15 lut 23:26
Mila: RRRRRRRRRRRRrrrr
15 lut 23:27
bezendu: I wyszło coś nie tak.
15 lut 23:28
Mila: Jak nie wyszło ? r2+(2r)2=|OB|2 |AO|=|OB|=r√5 Dalej myśl, wiadomości masz, tylko je wykorzystaj.
15 lut 23:33
Mila: Ramię? Ile?
15 lut 23:36
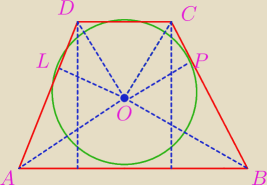
bezendu: rysunek |LO|=|OP|=r
15 lut 23:36
Eta: rysunek
 b 
r2=2r*
⇒ b=.....
 2 
15 lut 23:37
bezendu:
 √5r 
Druga odległość
?
 2 
15 lut 23:38
Eta: okemotka
15 lut 23:39
Mila: No i jest wszystko. emotka
15 lut 23:40
bezendu: Dobrze to zaraz koleje którego nie zrobiłem jeszcze.
15 lut 23:42
Eta: emotka emotka
15 lut 23:43
Mila: Dobranoc, miłej współpracy emotka
15 lut 23:45
bezendu: Oblicz długości boków trapezu równoramiennego opisanego na okręgu, znając obwód trapezu 4p i długość d jego przekątnej a+b+2c=4p Tyle zapisałem tylko
15 lut 23:45
bezendu: Dobranoc Mila i dziękuję za pomoc.
15 lut 23:46
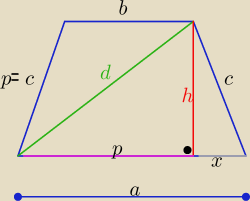
Eta: rysunek a+b=2c ⇒ 4c=4p ⇒ c=p
a+b 
= c=p h=√d2−p2 , x=√p2−h2=.......
2 
a=p+x =.... b= p−x=... dokończ .....
16 lut 00:24
bezendu: a=c+√x2−h2 b=c−√p2−h2 Tylko czemu tak ?
16 lut 00:29
Eta: zamiast c pisz "p" bo c=p
16 lut 00:31
bezendu: Do tego już doszedłem, ale jak wyliczyłaś x?
16 lut 00:32
Eta: Z tw. Pitagorasa x2=c2−h2 ⇒ x= √p2−(d2−p2)=......
16 lut 00:38
bezendu: Dziękuję.
16 lut 00:42
Eta: achhh emotka
16 lut 00:43
bezendu: Będziesz jutro po południu ?
16 lut 00:44
Eta: Tak emotka
16 lut 00:49
bezendu: To do jutra, dobranoc i oczywiście dziękuję.
16 lut 00:56
Eta: Miłych snów
16 lut 00:58